7. Характеристики системы случайных величин: центр распределения и матрица ковариаций. Связь между понятиями независимости и некоррелированности.

Две или несколько сл.вел. Х1,Х2,…,ХL образуют систему сл.величин. Система сл.вел. может рассматриваться как случ.вектор Х=( . Основными хар-ками системы случ. величин служат: центр распределения М= ) =( ) ; матрица ковариаций К=(Kij)= ( ), где a=М(Хi)-мат ожидание величины Xi (i=1,2,…,L); Kij=Kji-ковариация между величинами Xi, Xj (i,j=1,2,…,L,i не = j), Kij=cov(XiXj)=M[(Xi-ai)(Xj-aj)], Kii=D(Xi) –дисперсия величины Хi.

Ковариация м-дуXi, Xj для дискретных сл.вел. :Кij=M(XiXj)-aiaj= .

Две сл. величины Х и У являются(статистически) независимыми, если для любых ф-ций f(x) и g(x), для к-х сущ-ют м.о., имеет место соотношение: М[f(x)*g(x)]=M[f(x)]*M[g(x)]. Смысл этого определения состоит в том, что никакая информация о значениях одной величины не влияет на информацию о значениях другой величины. То есть, следует M[X*Y]=M(X)*M(Y), а так же то, что из независимости 2х сл.вел. следует их некоррелированность, т.е. если X и У независимы, то cov(X,Y)=0. Дисперсия линейной комбинации случ. величин выражается через ковариации:

D( = . В частности, для попарно независимых величин Хi и Xj ковариации Kij=0(i,j=1,2,…,L, i не = j) и матрица ковариаций диагональна, а дисперсия лин.комб. величин выражается только через их дисперсии D(

8. Дискретная случайная величина. Вычисление числовых характеристик. Биномиальное распределение.Опр. см в1. =) Вычисление числовых характеристик: см в.1, 6*** Биномиальное распределение:

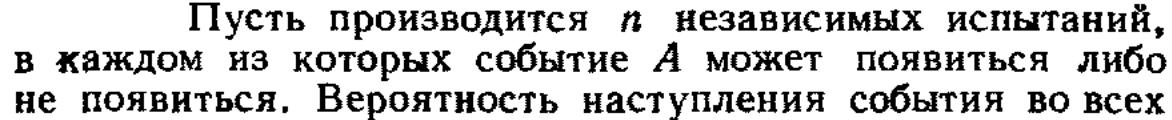
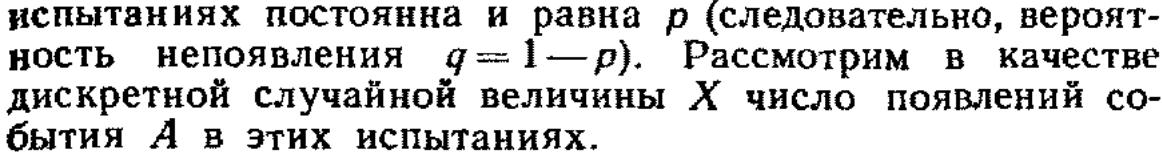
Рn(m) – вер-ть того, что что в n испытаниях соб. А наступит ровно m раз, тогда сл.вел. Х, такая, что Р(Х=m)= Рn(m) ,опред. биномиальное распределение или распределение Бернулли Рn(m)= = , где С – число сочетаний из n эл-тов по m и выч. по ф-ле: = n!/m!(n-m)!

Для бин.распред. М(Х)=pn, D(X)=pqn,q=1-p.

9. Непрерывные распределения вероятностей. Функция плотности вероятностей, ее свойства и применение. Функция распределения вероятностей, ее свойства и применение.

Функция наз-ся плотностью распределения вероятностей, непрерывной случайной величины Х и обладает след. свойствами: 1.Вероятность попадания величины Х в произвольный интервал на оси Ох равна P(X A) = M(IA)= ** т.е. интегралу А от ф-ции плотности. Т.О. ф-ция плотности 2. В частности, для интервала (x,x+

,получаем из ф-лы: Р(X (x,x+ = ; 3. Так как вер-ть неотрицательна, то из *

следует , что 4. Вероятность достоверного события равна 1, поэтому . График ф-ции плотности распределения наз-ся кривой распределения. Вероятность попадания сл.вел. Х в интервал (х1,х2) численно равна площади соотв. криволинейной трапеции. Из условия нормировки следует, что площадь области, ограниченной сверху кривой распределения, а снизу- осью Ox,равна 1. ВЕРОЯТНОСТЬ ПОПАДАНИЯ НЕПРЕРЫВНОЙ СЛ.ВЕЛ. В ЛЮБУЮ ОТДЕЛЬНУЮ ТОЧКУ РАВНА 0. Функцией распределения вероятностей сл.вел.Х наз-ся ф-ция F(x), равная вер-ти события (X<x), т.е. вер-ти того, что сл. вел. Х примет значение, меньшее значения аргумента х.

Для непрерывной сл.вел. ф-ция распределения равна: F(X)=P(X<x)= и обладает след. свойствами: 1) 0 1 для всех х; 2) F( F( =1;3) F(x)-неубывающая функция на всей оси; 4) F(x)-непрерывная ф-ция, в точках непрерывности F(x) непрерывна и кусочно-дифференцируема.

Вероятность попадания непрерывной случ. величины Х в произвольный интервал (х1;х2) можно вычислить с пом-ю ф-ции распределения след.образом: P(X

F(x2)-F(x1). ДОК-ВО: {X1<x2}={X<x1} {x1 }, F(x2)=P(X<x2)=P(X<x1)+P(x →P{x1 }= F(x2)-F(x1). Поэтому ф-ция распределения F(x) так же, как и ф-ция плотности распределения , полностью хар-ет распределение вероятностей сл.вел. Х.

В задачах статистики часто бывает нужно найти такое значение х по заданной вероятности Р, что Р=Р(Х<x)=F(x)*. Данное ур-е может иметь множ-во решений. Но для большинства распределений, встречающихся в статистике, ф-ция плотности распределения строго положительна для всех Х

из некоторого интервала и равна 0 вне этого интервала. Поэтому внутри этого интервала ф-ция F(x) строго монотонно возрастает. В этих случаях решение уравнения* сущ-ет и единственно для всех Р . Оно называется квантилью распределения и обозначается хр. Некоторые квантили имеют спец. название. Медианой непрерывной случайной величины Х наз-ся действительное число mX, удовлетворяющее условию Р(Х<mx)=P(X>mx)=0.5, т.е.является решением ур-я F(x)=0.5; mx=x0.5

10. Нормальное распределение вероятностей. Интеграл вероятностей.

11.Оценка математического ожидания при равноточных измерениях, несмещенность и состоятельность оценки.

12. Несмещенная оценка дисперсии

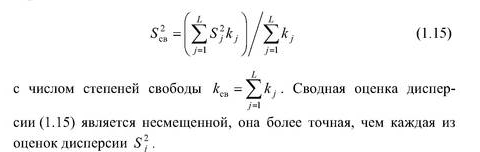
13. Распределение Стьюдента. Доверительный интервал для математического ожидания в случае известной и неизвестной дисперсии.

14. Распределение Пирсона. Доверительный интервал для среднего квадратического отклонения.

15. Алгоритм проверки статистических гипотез. Функция критерия. Уровень значимости. Ошибки первого и второго рода при проверке статистических гипотез.

16. Проверка гипотез о математическом ожидании. Односторонние и двусторонние критерии.

Проверка гипотезы о равенстве мат. ожид. двух выборок (критерий Стьюдента)

Пусть генеральные совокупности Х и У распределены по нормальным законам N( , ) и N , ). Дисперсии и неизвестны, но гипотеза о равенстве дисперсий принимается. Требуется при заданном уровне значимости проверить нулевую гипотезу : =

Пусть , -выборочные дисперсии. Сводная оценка дисперсии

В качестве критерия проверки нулевой гипотезы принимается случ. величина T=

=> ; =

Вида альтернативных гипотез:

1. : > Для случайной величины Т строят правостороннюю критическую область

Если Т< нулевая гипотеза принимается с уровнем значимости α.

2. : < строят левостороннюю критическую область

Гипотеза принимается при условии Т> с уровнем значимости α.

3. : ≠ строят двустороннюю критическую область из условия P{|T| > t(α,k)}=α

Нулевая гипотеза принимается при условии |Т|<

Замечание

Если дисперсии и известны, то в качестве критерия проверки нулевой гипотезы принимается случ. величина U= , которое имеет стандартное нормальное распределение (U~N(0,1))

Гипотеза о равенстве мат. ожид. принимается, если:

1. U< для : >

2. U> для : <

3. |U|< для : ≠

Проверка гипотезы о равенстве мат. ожид. заданному числу

Пусть –выборки из ген.совокупности, распределенной по нормальному закону Х~N(α,σ).

Значение мат. ожид. неизвестно. -оценка мат. ожидания. Требуется при заданном уровне значимости проверить нулевую гипотезу : a=

Пусть дисперсия неизвестна. В качестве критерия проверки нулевой гипотезы принимается случ. величина t = , которое имеет распределение Стьюдента с k степенями свободы.

Вида альтернативных гипотез:

1. : a> строят правостороннюю критическую область

Если t < нулевая гипотеза принимается с уровнем значимости α.

2. : a< строят левостороннюю критическую область

Гипотеза принимается при условии t> с уровнем значимости α.

3. : a≠ строят двустороннюю критическую область. Нулевая гипотеза принимается при условии |t|<

Замечание

Если дисперсия известна, то в качестве критерия проверки нулевой гипотезы принимается случ. величина U= , которое имеет стандартное нормальное распределение (U~N(0,1))

Гипотеза о равенстве мат. ожид. принимается, если:

1. U< для : a>

2. U> для : a<

3. |U|< для : a≠