4. Условные математические ожидания и условные вероятности. Правило умножения вер-тей

Условная вероятность. Выбор без возвращения: Обозначим Р(В/А)-вер-ть соб. В при условии, что произошло соб.А. Такая вер-ть наз-ся условной вероятностью. Аналогично введем Р(В/А), очевидно, что Р(В/А)=1/2,Р(В/А)=3/4. Вер-ть В зависит от того, произошло ли А.(в урне а шаров, 2б и 3ч.). Тогда Р(АВ)=3*2/5*4=3/10=Р(А)*Р(В). Р=Перейдем к опред. Условная вер-ть Р(В/А):применим статистический подход. Пусть опыт вторен N раз, при этом событие А наблюдалосьсь Na раз, событие AB-Nab раз. Условная частота появления события АВ в серии из Na опытов равна Nab/Na=(Nab/N)/(Na/N) P(AB)/P(A)

C др. стороны, при больших Na, Nab/Na P(B/A), поэтому ест-но применять по опред.: P(B/A)=P(AB)/P(A)

Правило умножения вероятностей: Р(АВ)=Р(А)Р(В/А).Следствие: 1) Р(А)Р(В/А)=Р(В)Р(А/В);

2) Р(А1А2…Аn)=P(A1)P(A2/A1)P(A3/A1A2)…P(An/A1A2…An-1).

5. Независимость случайных величин и событий.

Статистическая независимость:

6. Дисперсия случайных величин, свойства дисперсии.

Для хар-ки степени разбросанности значений сл.вел. около ее м.о. М(Х)=а вводятся понятия дисперсии D(X) и среднего квадратического отклонения : D(X)=M(X-a)^2; =

Св-ва дисперсии*** и ср.кв.отклонения ДИСКРЕТНОЙ величины:1) D(C)=0; , C=const;

2) D(CX)= C^2D(X);

3) D(X+Y)=D(X)+D(Y), если Х и У независимы. Дисперсия сл. вел. Х может быть вычислена по ф-ле: D(X) = M(X^2)-a^2=

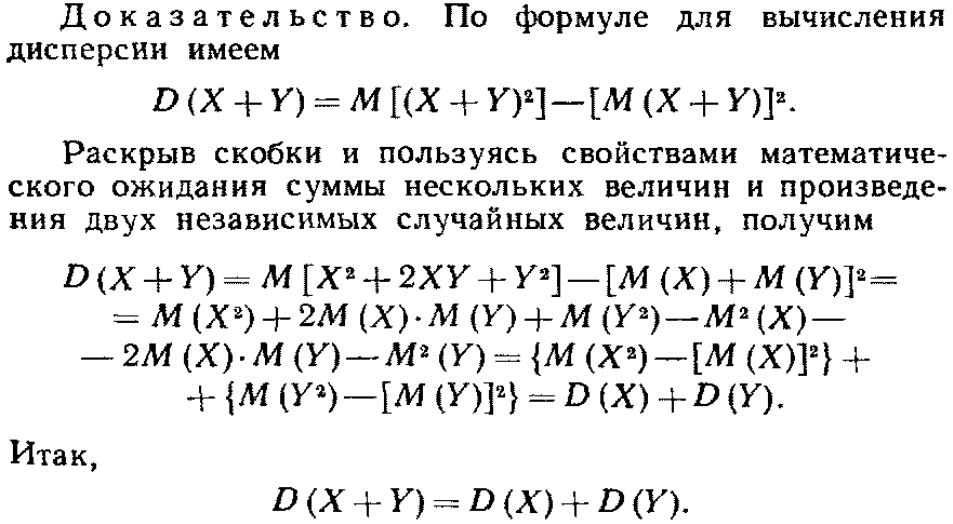
Дисперсия числа появления события в независимых испытаниях:

М.о. и дисперсия сл.вел., имеющей биномиальное распределении, могут быть найдены по ф-лам М(Х)=np; D(X)=npq, где p-вер-ть того, что соб.А произойдет, q-вер-то того, что соб.А не произойдет в каждом из независимых испытаний. Для распределения Пуассона М(Х) = D(X)= . Две или несколько сл.вел. Х1,Х2,…,ХL образуют систему сл.величин. Система сл.вел. может рассматриваться как случ.вектор Х=( . Основными хар-ками системы случ. величин служат: центр распределения М= ) =( ) ; матрица ковариаций К=(Kij)= ( ), где a=М(Хi)-мат ожидание величины Xi (i=1,2,…,L); Kij=Kji-ковариация между величинами Xi, Xj (i,j=1,2,…,L,i не = j), Kij=cov(XiXj)=M[(Xi-ai)(Xj-aj)], Kii=D(Xi) –дисперсия величины Хi.

Ковариация м-дуXi, Xj для дискретных сл.вел. :Кij=M(XiXj)-aiaj= .

Две сл. величины Х и У являются(статистически) независимыми, если для любых ф-ций f(x) и g(x), для к-х сущ-ют м.о., имеет место соотношение: М[f(x)*g(x)]=M[f(x)]*M[g(x)]. Смысл этого определения состоит в том, что никакая информация о значениях одной величины не влияет на информацию о значениях другой величины. То есть, следует M[X*Y]=M(X)*M(Y), а так же то, что из независимости 2х сл.вел. следует их некоррелированность, т.е. если X и У независимы, то cov(X,Y)=0. Дисперсия линейной комбинации случ. величин выражается через ковариации:

D( = 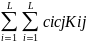. В частности, для попарно независимых величин Хi и Xj ковариации Kij=0(i,j=1,2,…,L, i не = j) и матрица ковариаций диагональна, а дисперсия лин.комб. величин выражается только через их дисперсии D(

Св-ва дисперсии НЕПРЕРЫВНОЙ.сл.в: D(X) = M(X-M(X))^2 = ;

D(X) = M(X^2)-(M(X))^2 = . Система случ.вел Х и У задается плотностью совместного распределения и формулы* и ** заменяются на: М[f(X,Y)]= P((X,Y) Если величины Х и У независимы, то = где -плотности распределения величин Х и У.