1. Случайные величины, их математические ожидания. Свойства математических ожиданий.
X |
х 1 |
х 2 |
… |
х n |
P |
p 1 |
p 2 |
… |
p n |
Где хi упорядочены по возрастанию,
х1<
x2<…<xn
и pi=P(X=xi).
Так как события Х=хi
образуют полную группу, то
,
что служит часто проверкой правильности
вычисления pi.
Случайные
величины могут описываться числовыми
хар-ками, среди к-х различают характеристики
положения(в частности мат.ожидание).
Математическое ожидание М(Х) представляет
собой среднее ожидаемое значение
случайно величины. Если пространство
элементарных исходов состоит из конечного
числа взаимно исключающих друг друга
возможных исходов w1,w2,…,wn
с вероятностями Р(wi)=pi(i=1,2,…,N;
то м.о. сл.вел. Х=Х(w)
выч.по ф-ле: М(Х)=
а вероятность случ. события А- по ф-ле:
Р(А)=М(IA)=
(wi
A),
где IA-индикатор
события А, т.е. случ. величина, принимающая
значение 1 при wi
A
и значение 0 при wi
не
А.
Св-ва мат. ожидания ДИСКР.сл.в.:1) М(С)=С, где С=const; 2) М(СХ)=СМ(Х); 3) М(Х+У)=М(Х)+М(У) для любых сл.вел. Х и У; 4) М(ХУ)=М(Х)*М(У), если Х и У независимы. Т.О. если случ. вел.Х представлена в виде лин. комбинации величин Х1,Х2,…,ХL, то ее м.о. выч-ют, пользуясь св-вом линейности:
М(Х)=М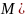
.
Если известна табл. распредел. Дискретной
сл.вел., то м.о. любой ее ф-ции можно
вычислить по ф-ле: М(f(X))=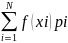
.
Непрерывной
наз-ют случ.величину,
к-я может принимать все значения, из
некоторого конечного или бесконечного
промежутка. Число возможных значений
непрерывной сл. величины бесконечно.
(строгое
определение:
случ.вел. наз-ся непрерывной,
если мат.ожиание любой функции g(X)
можно записать в виде:*
.
Под любой ф-ей g(x)
имеется ввиду такая, для которой интеграл*
сущ-ет и сходится абсолютно
Св-ва
мат. ожидания НЕПРЕРЫВНОЙ.сл.в.:
M(X)
=
;
Статистич.
Смысл М.О.: пусть pi=P{X=xi},
;
проводя n
независимых повторений опыта S,
причем X=xi
в ni
случаях (i=1,2,…,m)
.Тогда Хср=1\n
при n→
.
Естественно принять это значение за
теоретическое среднее величины Х в
эксперименте S.
ni\n-частота повторения события {X=xi}
M.O.
дискр. сл.вел. наз-ся сумма произведений
всех ее возможных значений на их
вероятности. M(X)=
.
Свойства М.О.(Л)
1. Если в- неслучайная величина, то М(в)=в. ДОК-ВО: М(в)=в*1=в(рассм. Пост.величину как дискретную случ. величину, принимающую одно и то же значение с вероятностью р=1)
2.
Если а- неслуч. вел., т.е. явл-ся константой,
то М(ах)=аМ(х) ДОК-ВО:
М(аХ)=
.
3. М.о. суммы двух случ. величин равно сумме мат. О. слагаемых(св-во линейности) М(Х+Н)=М(Х)+
М(У) ДОК-ВО: пусть Х принимает значения Хi(i=1,2,…,n) с вероятностью pi, сл-но величина У принимает значения Уi (i=1,2,…,n) с вероятностью qi. Событие, состоящее в том, что сл. величина Х примет значения xi (i=1,2,…,n) с вероятностью pi влечет за собой событие, к-е состоит в том, что сл. вел. Х+У примет значения xi+y1,…xi+yk (i=1,2,…,n), вероятность которого по т. О сложении вер-тей
pi1+…+pik=pi. Аналогично, qj=p1j+…+pnj
M(X+Y)=(x1+y1)p11+(x1+y1)p12+…+(x1+yk)p1k+(x2+y1)p21+(x2+y2)p22+…+(x2+yk)p2k+…+(xn+
+y1)pn1+(xn+y2)pn2+…+(xn+yk)pnk=x1(p11+p12+…+p1k)+x2(p21+p22+…+p2k)+…+xn(pn1+pn2+.)=
=x1p1+x2p2+…+xnpn+y1q1+y2q2+…xnpn+y1q1+y2q2+ykqk=M(X)+M(Y)
4.
Случ. вел. Х и У наз-ся НЕЗАВИСИМЫМИ,
если
для любых ф-циё f(x)
и g(x)
→ М(g(X)*f(Y))=
=M(g(X))*M(f(Y)).
Ни какая инфа об одной с.в. не влияет на
значение др. В частности, М(ХУ)=М(Х)*М(У).
По определению, М(g(X))=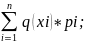
pi=P{X=xi}
5. М.о. произведения нескольких независимых случ. величин равно произведению их мат. ожиданий;
6. М.о. суммы нескольких случ. величин равно сумме их мат. ожиданий.
7.
М(
Вероятностный смысл М.О.: среднее арифметическое с учетом вероятности.
Замечание:
1) М.О. дискр. сл.вел.- это неслучайная вел.(константа)
2) М.О. больше наименьшего и меньше наибольшего из возм-х значений сл.вел., то есть на числовой оси возм-е значения располагаются слева и справа от М.О. В этом смысле м.о. хар-ет распределение случ.вел. и поэтому наз-ся центром распределения.
3) М.О.-число, около к-го группируется ср.арифметическое в большой серии измерений. (пример:измерение какого-либо предмета. М.
