22Ламинарный режим течения. Течение Пуазейля. Решение уравнений Навье-Стокса для течения в плоской щели.

Лам. режим течен. – реж. теч., при котором слои жидкости двужутся не перемеш., а линии тока имеют вполне гладкий и упорядоч. характер. В вязк. жидк. происх. деформац. частиц, и их движ. при этом имеет и поступ. и вращат. состоавляющие. Однако линии тока имеют «предсказуемый» характер и УНС всегда справедливы. Сила вязкости оказ. сглаживающ.,стабилизирующ. влиян. на поток. Однако при повышении крит. числа Re лам. реж. теч. станов. неустойчивым –малые возмущ. поля скор. нараст.,что влечёт за собой переход к турб. реж. теч.

Рассмотрим модель плоского течения Пуайзеля,в кот. реализ. простое,хотя и неоднор.,напр. сост. жидк.

Представл. график напряж. τ и профиль скоростей v(y) в завис. от расстояния(толщины) у.

Пусть жидк. течет м/у двумя неподв. тв. плоскостями под действ. пост. градиента давления. Такое дв. наз. плоским теч. Пуайзеля.

Для вычисл. скор. жидкости восп. гипот. Ньютона: . Получим:

В качестве граничного здесь использованы усл. «прилипания» жидк. к тв. стенке: v=0 при у=0,h

Пусть треб. найти распр. скоростей и давл. в плоском канале(щели) высотоой h при установивш. теч. жидк. с ρ=const и μ=const. В этом случ. можно искл. из рассмотр. z и v_z, а также описать дв. ур. неразр. и ур. дв. по х и у, так что иск. функц. будут лишь р(х,у),v_x(х,у),v_y(х,у). Распишем УНС в проекц. на оси х и у:

; ;

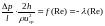
23.Устойчивость ламинарного движения и его переход к турбулентному.

Переход от ламинарного течения к турбулентному имеет характер развития неустойчивости в потоке. Нач. возмущ. любого рода,вводим. в лам поток,может как сойти на нет,так и привести к развитию турбулентности. Малые значение числа Рейнольдса гов. о том,что возмущ. в форме появивш. вихря будет сглаж. Для каждого течения существует такой диапазон чисел Re, в кот. набл. переход от лам. к турб. Есть нижн. предел числа Re=Re_кр для которого режим теч. будет оставаться ламинарным.

1-лам.,2-переходн.,3-турб.

Течение в переходной области не является стабильным. Турбулентность появляется в некоторой части пограничного слоя, затем турбулентно текущая жидкость уносится потоком. Смена ламинарных и турбулентных состояний течения происходит через неравномерные промежутки времени. Такое перемежающееся течение характеризуют коэффициентом перемежаемости ω. Коэффициент перемежаемости указывает, какую долю некоторого промежутка времени в определенной области жидкости существует турбулентное течение. Следовательно, коэффициент ω=1 означает, что течение все время турбулентное, а коэффициент ω=0 показывает, что течение все время ламинарное. Таким образом, граничные значения x_kр1 и x_kр2 приобретают характер осредненных во времени значений.

24.Турбулентное течение. Число Рейнольдса. Критическое число Рейнольдса.

Турб. наз. режим течения жидк. или газа, при кот. парам. потока в рассматрив. обл. претерпевают пульсации во времени, причин. кот. явл. кажущееся беспорядочным движен. вихревых структур, сущ. в более ли менее широком интервале масштабов по пространству и во времени. В развит. турб. реж. осн. теч порождает вихри,кот. наклад. на осн. теч.,имеют тенденц. к измельчен. Нижний предел масштаба таких вихрей наз. колмогоровским. В отл. от ламинарн. траект частиц турб. теч. имеют извилистый, непредск. хар.

- число Р. опр. по среднерасходной скор. uср и высоте h плоского канала. Это безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье-Стокса. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.

Для каждого течения существует такой диапазон чисел Re, в кот. набл. переход от лам. к турб. Есть нижн. предел числа Re=Reкр для которого даже при налич. возмущ. режим теч. будет оставаться ламинарным. Несколько большим значен. Re>Reкр отвечают место переходн. режимы течен.,для кот. характерно чередов. в одном месте трубы периодов более-менее развитого турб. теч. и периодов «реламинаризации». При дост. больших зн. числа Re режим теч. в трубах становится устойчиво турбулентным.