
- •1.Научная дисциплина «Механика жидкости и газа». Ее место в системе естественнонаучных знаний.
- •2.Основные гипотезы мжг гипотеза сплошности и гипотеза о локальном термодинамическом равновесии.
- •3.Изучение движения сплошной среды в переменных Эйлера и в переменных Лагранжа.
- •4.Уравнения состояния. Идеальный и совершенный газ. Отношение теплоемкостей. Уравнения состояния капельных жидкостей.
- •5.Силы, действующие в сплошной среде. Нормальные и касательные напряжения. Тензор напряжений. Тензор вязких напряжений.
- •6.Силы, действующие в жидкости. Гипотеза Ньютона. Коэффициент вязкости. Обобщенная гипотеза Ньютона. «Ньютоновские» и реологические жидкости.
- •7.Модели жидкой среды. Несжимаемая и сжимаемая жидкость. Идеальная и вязкая жидкость.
- •12. Уравнения движения в напряжениях. Уравнения гидростатики.
- •13. Сила гидростатического давления. Равнодействующая гидростатических сил. Закон Архимеда.
- •15. Уравнения в форме Громеки-Лэмба. Преобразуем уравнения
- •16.Интегралы Коши-Лагранжа и Бернулли.
- •17.Тензор напряжений в идеальной жидкости. Потенциальное движение
- •18. Динамика идеальной жидкости. Теоремы Томсона и Гельмгольца.
- •19.Парадокс Даламбера.
- •20.Гипотеза Ньютона. Обобщенная гипотеза Ньютона. Закон Фика. Число Прандтля. Уравнения Навье-Стокса для сжимаемой среды.
- •21.Уравнения Навье-Стокса для несжимаемой среды.
- •22Ламинарный режим течения. Течение Пуазейля. Решение уравнений Навье-Стокса для течения в плоской щели.
- •23.Устойчивость ламинарного движения и его переход к турбулентному.
- •24.Турбулентное течение. Число Рейнольдса. Критическое число Рейнольдса.
- •25.Подходы к математическому моделированию турбулентных течений.
- •26.Методология расчета осредненного турбулентного течения. Осреднение уравнений Навье-Стокса по Рейнольдсу и по Фавру.
- •31. Свободная турбулентность. Теория локально изотропной турбулентности Колмогорова-Обухова.
- •32. Пристенное турбулентное движение.
- •33. Течение жидкости и газа по трубам. Коэффициент потерь на трение (формула Дарси-Вейсбаха).
- •34. Течение жидкости и газа по трубам. Напряжение и тепловой поток на стенке. Аналогия Рейнольдса.
- •35. Режимы течения жидкости и газа по трубам. Вывод формул для коэффициентов потерь. Формулы Блазиуса и Никурадзе.
- •41.Соотношения для осредненных профилей скорости, температуры, концентрации в свободных турбулентных струях.
- •42.Размерные и безразмерные величины. Функциональные связи.
- •44.Подобие. Условия подобия. Числа подобия. Критерии подобия
- •45.Подобие при течении жидкостей в пс и в трубах. Условия подобия при обтекании тел
- •46. Особенности до- и сверхзвуковых пространственных течений газов.
- •47. Законы сохранения для стационарных течениях одномерном приближении.
- •48. Течение в идеальном сопле (канале). Параметры и газодинамические функции стационарного торможения. Число м.
- •49.Течение в идеальном сужающемся сопле. Критический режим и критическая скорость. Приведенная скорость λ.
- •50.Сверхзвуковое течение. Задача о стационарном истечении в вакуум.
- •54. Потери полного давления на скачке уплотнения. Адиабата Гюгонио
- •57. Задание начальных и граничных условий в задачах нестационарной газовой динамики.
- •58.Параметры и газодинамические функции нестационарного торможения.
- •59.Волны конечной амплитуды (вка). Простые и изоэнтропные вка. Соотношения при переходе через фронт изоэнтропной вка.
- •61. Воздействие на уединенную вка профилированием трубопровода по длине.
- •62.Отражение вка от открытого и от закрытого концов трубопровода.
- •63.Закономерности наполнения и опорожнения емкости через трубопровод («кривошипная камера», «ресивер», «цилиндр»).
- •64.Генерирование вка движущимся поршнем. Задача о нестационарном истечении в вакуум.
- •65. Задача о распаде произвольного разрыва.
- •66. Распад разрыва на скачке сечения.
- •67.Распад разрыва на стыке емкости и канала.
- •68. Распад разрыва при отводе и подводе энергии в форме работы.
- •69. Распад разрыва на отверстии в боковой стенке канала.
- •70. Распад разрыва в месте разветвления.
- •71. Метод характеристик и сеточно-характеристический метод.
- •72. Метод распада произвольного разрыва с. К. Годунова.
- •73.Метод Годунова для решения пространственных задач мжг по уравнениям Эйлера.
17.Тензор напряжений в идеальной жидкости. Потенциальное движение
В несжимаемой идеальной жидкости, где div v ≡ 0, тензор вязких напряжений имеет вид
![]()
а тензор напряжений
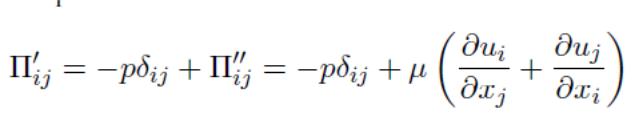
На первый взгляд отсюда можно было бы сделать следующий вывод. Рассмотрим стационарное обтекание какого-либо тела потоком жидкости. На бесконечности натекающий поток однороден; его скорость v = const, так что rot v ≡ 0 на всех линиях тока. Отсюда можно было бы заключить, rot v будет равен нулю и вдоль всей длины всех линий тока, т. е. во всем пространстве.
Движение жидкости, при котором во всем пространстве rot v = 0, называется потенциальным (или безвихревым) в противоположность вихревому движению, при котором ротор скорости отличен от нуля. Таким образом, мы пришли бы к результату, что стационарное обтекание всякого тела натекающим из бесконечности однородным потоком должно быть потенциальным.
18. Динамика идеальной жидкости. Теоремы Томсона и Гельмгольца.
Теорема Кельвина (В. Томсона) о циркуляции скорости: При баротропном течении идеальной жидкости под действием поля
массовых сил с однозначным потенциалом циркуляция скорости
по замкнутому жидкому контуру не изменяется.
Или: Если силы, действующие в баротропной жидкости, име-
ют потенциал, то циркуляция скорости по любому жидкому кон-
туру не изменяется с течением времени:
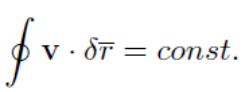
Теорема разложения Гельмгольца — утверждение о разложении произвольного дифференцируемого векторного поля на две компоненты:
-
Если дивергенция и ротор векторного поля
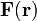 определены
в каждой точке конечной открытой
области V пространства, то всюду в V
функция может быть представлена в
виде суммы безвихревого поля
определены
в каждой точке конечной открытой
области V пространства, то всюду в V
функция может быть представлена в
виде суммы безвихревого поля
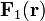 и
соленоидального поля
и
соленоидального поля
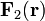 :
: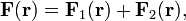
где
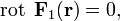
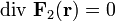
для всех точек
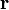 области
V.
области
V.
19.Парадокс Даламбера.
Парадокс Даламбера: сопротивление Fx тела, равномерно движущегося в идеальной безграничной жидкости, равно нулю (как и подъемная сила Fy).
Строгого доказательства приводить не будем, отметим очевидность
этого явления для тел симметричной формы типа цилиндра, шара, эллипсоида — струйки тока расступаются на обращенной против потока
поверхности, и картина эта в точности повторяется и на задней поверхности (в правом полупространстве на рис. НЕТ). Распределение гидро-
динамических давлений по поверхности симметрично, интеграл силы равен нулю. При этом на поверхность тела не действуют касательные напряжения; в объеме потока не протекают процессы диссипации энергии и ее волнового перераспределения по пространству, поэтому при относительном перемещении тела в такой жидкости и не должна совершаться работа, следовательно, сопротивление равно нулю. В силу фундаментальности подобных оснований нет причин, чтобы для тел иной формы, по крайней мере, лобовое сопротивление имело бы место. При нарушении хотя бы одного из указанных выше условий равенство нулю исчезает:
• вязкость — возникнут касательные напряжения, вязкая диссипация энергии в объеме;
• сжимаемость—возникнут упругие возмущения (волны), уносящие
энергию;
• свободная поверхность или границы-стенки —возникнут поверх-
ностные волны и ???;
• нестационарность — потребуется энергия на распространение
возмущения (разгон) слоев жидкости;
