
- •1.Научная дисциплина «Механика жидкости и газа». Ее место в системе естественнонаучных знаний.
- •2.Основные гипотезы мжг гипотеза сплошности и гипотеза о локальном термодинамическом равновесии.
- •3.Изучение движения сплошной среды в переменных Эйлера и в переменных Лагранжа.
- •4.Уравнения состояния. Идеальный и совершенный газ. Отношение теплоемкостей. Уравнения состояния капельных жидкостей.
- •5.Силы, действующие в сплошной среде. Нормальные и касательные напряжения. Тензор напряжений. Тензор вязких напряжений.
- •6.Силы, действующие в жидкости. Гипотеза Ньютона. Коэффициент вязкости. Обобщенная гипотеза Ньютона. «Ньютоновские» и реологические жидкости.
- •7.Модели жидкой среды. Несжимаемая и сжимаемая жидкость. Идеальная и вязкая жидкость.
- •12. Уравнения движения в напряжениях. Уравнения гидростатики.
- •13. Сила гидростатического давления. Равнодействующая гидростатических сил. Закон Архимеда.
- •15. Уравнения в форме Громеки-Лэмба. Преобразуем уравнения
- •16.Интегралы Коши-Лагранжа и Бернулли.
- •17.Тензор напряжений в идеальной жидкости. Потенциальное движение
- •18. Динамика идеальной жидкости. Теоремы Томсона и Гельмгольца.
- •19.Парадокс Даламбера.
- •20.Гипотеза Ньютона. Обобщенная гипотеза Ньютона. Закон Фика. Число Прандтля. Уравнения Навье-Стокса для сжимаемой среды.
- •21.Уравнения Навье-Стокса для несжимаемой среды.
- •22Ламинарный режим течения. Течение Пуазейля. Решение уравнений Навье-Стокса для течения в плоской щели.
- •23.Устойчивость ламинарного движения и его переход к турбулентному.
- •24.Турбулентное течение. Число Рейнольдса. Критическое число Рейнольдса.
- •25.Подходы к математическому моделированию турбулентных течений.
- •26.Методология расчета осредненного турбулентного течения. Осреднение уравнений Навье-Стокса по Рейнольдсу и по Фавру.
- •31. Свободная турбулентность. Теория локально изотропной турбулентности Колмогорова-Обухова.
- •32. Пристенное турбулентное движение.
- •33. Течение жидкости и газа по трубам. Коэффициент потерь на трение (формула Дарси-Вейсбаха).
- •34. Течение жидкости и газа по трубам. Напряжение и тепловой поток на стенке. Аналогия Рейнольдса.
- •35. Режимы течения жидкости и газа по трубам. Вывод формул для коэффициентов потерь. Формулы Блазиуса и Никурадзе.
- •41.Соотношения для осредненных профилей скорости, температуры, концентрации в свободных турбулентных струях.
- •42.Размерные и безразмерные величины. Функциональные связи.
- •44.Подобие. Условия подобия. Числа подобия. Критерии подобия
- •45.Подобие при течении жидкостей в пс и в трубах. Условия подобия при обтекании тел
- •46. Особенности до- и сверхзвуковых пространственных течений газов.
- •47. Законы сохранения для стационарных течениях одномерном приближении.
- •48. Течение в идеальном сопле (канале). Параметры и газодинамические функции стационарного торможения. Число м.
- •49.Течение в идеальном сужающемся сопле. Критический режим и критическая скорость. Приведенная скорость λ.
- •50.Сверхзвуковое течение. Задача о стационарном истечении в вакуум.
- •54. Потери полного давления на скачке уплотнения. Адиабата Гюгонио
- •57. Задание начальных и граничных условий в задачах нестационарной газовой динамики.
- •58.Параметры и газодинамические функции нестационарного торможения.
- •59.Волны конечной амплитуды (вка). Простые и изоэнтропные вка. Соотношения при переходе через фронт изоэнтропной вка.
- •61. Воздействие на уединенную вка профилированием трубопровода по длине.
- •62.Отражение вка от открытого и от закрытого концов трубопровода.
- •63.Закономерности наполнения и опорожнения емкости через трубопровод («кривошипная камера», «ресивер», «цилиндр»).
- •64.Генерирование вка движущимся поршнем. Задача о нестационарном истечении в вакуум.
- •65. Задача о распаде произвольного разрыва.
- •66. Распад разрыва на скачке сечения.
- •67.Распад разрыва на стыке емкости и канала.
- •68. Распад разрыва при отводе и подводе энергии в форме работы.
- •69. Распад разрыва на отверстии в боковой стенке канала.
- •70. Распад разрыва в месте разветвления.
- •71. Метод характеристик и сеточно-характеристический метод.
- •72. Метод распада произвольного разрыва с. К. Годунова.
- •73.Метод Годунова для решения пространственных задач мжг по уравнениям Эйлера.
7.Модели жидкой среды. Несжимаемая и сжимаемая жидкость. Идеальная и вязкая жидкость.
Под жидкостью понимается газ/смесь газов или капельная жидкость. Структурной единицей любой жидкости в МЖГ является молекулярная частица (молекула, атом, электрон, ион). Для возможности изучать движение жидкости как сплошной среды в МЖГ принимаются две исходные гипотезы фундаментального характера – гипотеза сплошности и гипотеза о локальном термодинамическом равновесии. Первая из гипотез позволяет перейти к континуальному представлению характеристик сплошной среды от прерывистой картины, состоящей из индивидуальных структурных элементов. Вторая гипотеза, позволяя считать термодинамическое состояние в любой точке среды локально равновесным, разрешает использовать уравнения состояния обычного вида для замыкания в моделях МЖГ. Для задания физических свойств требуется задать уравнения состояния и использовать модельные гипотезы о способе учета в континуальном представлении явлений переноса на молекулярном масштабе (закон Ньютона, закон Фурье). Задав все вышеперечисленные соотношения, мы тем самым зададим конкретную модель жидкой среды.
Несжимаемая и сжимаемая жидкость. Все реальные жидкости обладают сжимаемостью, причем величина плотности , вообще говоря, зависит как от давления, так и от температуры. Повышение T при p = const приводит к уменьшению («температурное» расширение), при повышении p (в изотермическом — T = const или изоэнтропном — s = const процессах) также повышается плотность («нормальная» сжимаемость).
Малыми вариациями в потоке при решении задач методами МЖГ часто пренебрегают, используя модель несжимаемой жидкости. Эта модель задается условием = const — простейшим из возможных УС, выражающим свойство такой гипотетической жидкости не изменять ни при каких изменениях p и T. Основная особенность несжимаемой жидкости — бесконечная скорость распространения упругих возмущений, что формально следует из условия = const.
Идеальная и вязкая жидкость. Простейшей моделью текучей среды является модель идеальной жидкости – среды, обладающей при движении свойством идеальной текучести. Это означает отсутствие каких-либо дополнительных напряжений, возникающих вследствие деформации ее частиц.
Движение вязкой жидкости - движение сплошной изотропной среды, в которой возникают как нормальные, так и касательные напряжения. Движение происходит под действием сил двух видов: массовых сил, которые пропорциональны массе частицы и в аэро- и гидродинамических задачах являются заданными величинами, и поверхностных сил, которые возникают в результате взаимодействия соседних объёмов жидкости и характеризуются вектором напряжений.
8.Уравнение сохранения массы. Интегральная, дифференциальная (дивергентная) и «тензорная» формы записи.
 закон
сохранения массы в интегральной форме
закон
сохранения массы в интегральной форме
 закон
сохранения массы в дифференциальной
(дивергентной) форме
закон
сохранения массы в дифференциальной
(дивергентной) форме
 закон
сохранения массы в тензорной форме
закон
сохранения массы в тензорной форме
9.Уравнения сохранения количества движения. Интегральная, дифференциальная (дивергентная) и «тензорная» формы записи.
 закон
сохранения количества движения в
интегральной форме
закон
сохранения количества движения в
интегральной форме
 закон
сохранения количества движения в
дифференциальной форме
закон
сохранения количества движения в
дифференциальной форме
 закон
сохранения количества движения в
тензорной форме
закон
сохранения количества движения в
тензорной форме
10.Уравнение сохранения энергии. Интегральная, дифференциальная (дивергентная) и «тензорная» формы записи.
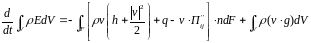
Уравнение сохранения энергии в интегральной форме, где
q – плотность теплового потока, h – удельная энтальпия
 Уравнение
сохранения энергии в дифференциальной
форме
Уравнение
сохранения энергии в дифференциальной
форме
 Уравнение
сохранения энергии в тензорной форме
Уравнение
сохранения энергии в тензорной форме
11.Интегральные законы сохранения при неустановившемся течении по трубопроводу в одномерной постановке.
Законы
сохранения в одномерном приближении.
Нестационарные (неустановившиеся)
течения сжимаемых жидкостей на
участках каналов имеет волновой
характер.
Изменения искомых параметров потока в
такой постановке изучаются в пространстве
двух независимых
переменных
 и
т.д.- координаты х,
отсчитываемой
вдоль слабо искривленной оси более или
менее протяженного канала, а так же во
времени t.
Будем
называть такие течения сжимаемых
жидкостей и газов одномерными
нестационарными.
и
т.д.- координаты х,
отсчитываемой
вдоль слабо искривленной оси более или
менее протяженного канала, а так же во
времени t.
Будем
называть такие течения сжимаемых
жидкостей и газов одномерными
нестационарными.
Основой моделей течений является система интегральных законов сохранения, в которые входят осредненные по сечению канала термогазодинамические параметры потока. Вывод ЗС для 1D течений основан на гипотезах о сплошности и о локальном термодинамическом равновесии в физически малых объемах смеси.Также принимается, что локальные значения средних но периметру напряжений трения τw и теплового потока qw на стенке канала распространяются мгновенно на все поперечное сечение, а но нормали на стенку действует термодинамическое давлению р в данном сечении.
 интегральное
уравнение сохранения массы k-го
компонента смеси при нестационарном
движении в канале (k
=
1...K).
интегральное
уравнение сохранения массы k-го
компонента смеси при нестационарном
движении в канале (k
=
1...K).



Или в более компактной форме, используя символические «векторные» обозначения:

