64.Генерирование вка движущимся поршнем. Задача о нестационарном истечении в вакуум.

Рассмотрим задачу о поршне — перегородке в исходно неподвижном газе, мгновенно при­водимой в движение с постоянной скоростью. Возникающие в газе возмущения — простые волны. В газе, по отношению к которому поршень вдвигается, будет распространяться про­стая волна сжатия со скачком уплотнения на фронте. В противоположном направлении (от поршня, который выдвигается из газа) образуется простая изоэнтропная ВКА имеющая вид

центрированной волны разрежения (ЦВР) — волны, все характеристики во фронте которой есть прямые лучи, выходящие из одной точки плоскости (х, t) (см. рис. 22). Рассмотрим дан­ный случай подробнее.

Здесь голова ЦВР (х = х_г) движется влево по неподвижному газу (параметры с индексом «1») со скоростью звука в нем, т. е. скорость головной элементарной волны разрежения (равная наклону характеристики) u₁ -C₁ равна всегда (—C₁), так как здесь щ = 0. Давление за хвостом (х = х₁) фронта волны (в зоне с постоянными параметрами) определяется скоростью поршня u_n > 0, но ход профиля давления (и др. параметров потока) между х_t и х_х от и_п не зависит.

При достаточно малых u_n распространяется волна акустического диапазона, голова и хвост ее фронта практически совпадают. При дальнейшем увеличении u_n хвост начинает заметно отставать, находясь все же в левом полупространстве — распространяется простая ВКА вида ЦВР. Звуковая скорость течения в зоне за ЦВР (вплоть до слоя газа, примыкающего к поршню) достигается при u_ПЭB = с_n . Воспользуемся условиями постоянства инварианта Римана I+„ = I+ j и энтропии частиц в ЦВР и найдем потребную для этого скорость поршня u

При еще больших значениях u_n поршень оторвется от газа и между ними образуется зона вакуума. Такой режим называется режимом нестационарного истечения в вакуум.

Параметры состояния газа в точке на хвосте ЦВР (на границе с вакуумом) примут нулевые значения (в соответствии с уравнением изоэнтропы для идеального совершенного газа). Скорость газа в этой точке и_{n вак} можно также определить по условию I₊₁ =I_{+ n} здесьI_{+ n} = и_{n вак} при с_п — 0; скорость и_{n вак} есть минимальная потребная для реализация режима истечения в вакуум скорость поршня. Имеем:

Полученная скорость ничтожной части частиц при нестационарной истечении в вакуум превышает скорость стационарного истечения в вакуум всего потока — при равных парамет­рах невозмущенного газа — вследствие каскадной передачи энергии в волне; согласно (90), в стационарном случае

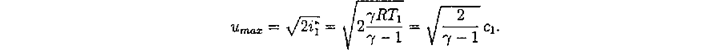
Для газа γ= 1,40 отношение максимальных скоростей нестационарного и стационарного истечения в вакуум составляет ≈ 2,24 раза.

Задача о наполнении вакуумированной емкости. Нетрудно показать, что при напол­нении исходно вакуумированной емкости совершенным газом через отверстие, температура газа в ней в 7 раз превышает температуру в окружающей атмосфере: T₂ = γТ1

Действительно, с самого начала (m= 0 кг, Е₂ = 0 Дж) каждая элементарная порция массы dm2, попадая в емкость, вносит туда порцию энергии, приводящую к увеличению внутренней энергии газа в ней: dE₂ = h(T\)dm2. В результате в любой момент процесса наполнения e₂= Е₂/m2 =h₁ а учитывая, что Е2=m₂e₂ т^е2> а также е=с_vТ и h=СрТ (для совершенного газа), очевидна справедливость равенства Т2 = (Ср/с_р)Т₁ =γT.

Другими словами, при пересечении частицами газа границы атмосферы и емкости следует учитывать (помимо внутренней энергии частиц) и работу проталкивания^ которую подсистема- атмосфера совершает над подсистемой-емкостью.