
- •1.Научная дисциплина «Механика жидкости и газа». Ее место в системе естественнонаучных знаний.
- •2.Основные гипотезы мжг гипотеза сплошности и гипотеза о локальном термодинамическом равновесии.
- •3.Изучение движения сплошной среды в переменных Эйлера и в переменных Лагранжа.
- •4.Уравнения состояния. Идеальный и совершенный газ. Отношение теплоемкостей. Уравнения состояния капельных жидкостей.
- •5.Силы, действующие в сплошной среде. Нормальные и касательные напряжения. Тензор напряжений. Тензор вязких напряжений.
- •6.Силы, действующие в жидкости. Гипотеза Ньютона. Коэффициент вязкости. Обобщенная гипотеза Ньютона. «Ньютоновские» и реологические жидкости.
- •7.Модели жидкой среды. Несжимаемая и сжимаемая жидкость. Идеальная и вязкая жидкость.
- •12. Уравнения движения в напряжениях. Уравнения гидростатики.
- •13. Сила гидростатического давления. Равнодействующая гидростатических сил. Закон Архимеда.
- •15. Уравнения в форме Громеки-Лэмба. Преобразуем уравнения
- •16.Интегралы Коши-Лагранжа и Бернулли.
- •17.Тензор напряжений в идеальной жидкости. Потенциальное движение
- •18. Динамика идеальной жидкости. Теоремы Томсона и Гельмгольца.
- •19.Парадокс Даламбера.
- •20.Гипотеза Ньютона. Обобщенная гипотеза Ньютона. Закон Фика. Число Прандтля. Уравнения Навье-Стокса для сжимаемой среды.
- •21.Уравнения Навье-Стокса для несжимаемой среды.
- •22Ламинарный режим течения. Течение Пуазейля. Решение уравнений Навье-Стокса для течения в плоской щели.
- •23.Устойчивость ламинарного движения и его переход к турбулентному.
- •24.Турбулентное течение. Число Рейнольдса. Критическое число Рейнольдса.
- •25.Подходы к математическому моделированию турбулентных течений.
- •26.Методология расчета осредненного турбулентного течения. Осреднение уравнений Навье-Стокса по Рейнольдсу и по Фавру.
- •31. Свободная турбулентность. Теория локально изотропной турбулентности Колмогорова-Обухова.
- •32. Пристенное турбулентное движение.
- •33. Течение жидкости и газа по трубам. Коэффициент потерь на трение (формула Дарси-Вейсбаха).
- •34. Течение жидкости и газа по трубам. Напряжение и тепловой поток на стенке. Аналогия Рейнольдса.
- •35. Режимы течения жидкости и газа по трубам. Вывод формул для коэффициентов потерь. Формулы Блазиуса и Никурадзе.
- •41.Соотношения для осредненных профилей скорости, температуры, концентрации в свободных турбулентных струях.
- •42.Размерные и безразмерные величины. Функциональные связи.
- •44.Подобие. Условия подобия. Числа подобия. Критерии подобия
- •45.Подобие при течении жидкостей в пс и в трубах. Условия подобия при обтекании тел
- •46. Особенности до- и сверхзвуковых пространственных течений газов.
- •47. Законы сохранения для стационарных течениях одномерном приближении.
- •48. Течение в идеальном сопле (канале). Параметры и газодинамические функции стационарного торможения. Число м.
- •49.Течение в идеальном сужающемся сопле. Критический режим и критическая скорость. Приведенная скорость λ.
- •50.Сверхзвуковое течение. Задача о стационарном истечении в вакуум.
- •54. Потери полного давления на скачке уплотнения. Адиабата Гюгонио
- •57. Задание начальных и граничных условий в задачах нестационарной газовой динамики.
- •58.Параметры и газодинамические функции нестационарного торможения.
- •59.Волны конечной амплитуды (вка). Простые и изоэнтропные вка. Соотношения при переходе через фронт изоэнтропной вка.
- •61. Воздействие на уединенную вка профилированием трубопровода по длине.
- •62.Отражение вка от открытого и от закрытого концов трубопровода.
- •63.Закономерности наполнения и опорожнения емкости через трубопровод («кривошипная камера», «ресивер», «цилиндр»).
- •64.Генерирование вка движущимся поршнем. Задача о нестационарном истечении в вакуум.
- •65. Задача о распаде произвольного разрыва.
- •66. Распад разрыва на скачке сечения.
- •67.Распад разрыва на стыке емкости и канала.
- •68. Распад разрыва при отводе и подводе энергии в форме работы.
- •69. Распад разрыва на отверстии в боковой стенке канала.
- •70. Распад разрыва в месте разветвления.
- •71. Метод характеристик и сеточно-характеристический метод.
- •72. Метод распада произвольного разрыва с. К. Годунова.
- •73.Метод Годунова для решения пространственных задач мжг по уравнениям Эйлера.
46. Особенности до- и сверхзвуковых пространственных течений газов.
Дозвуковое течение в идеальном диффузоре или конфузоре.
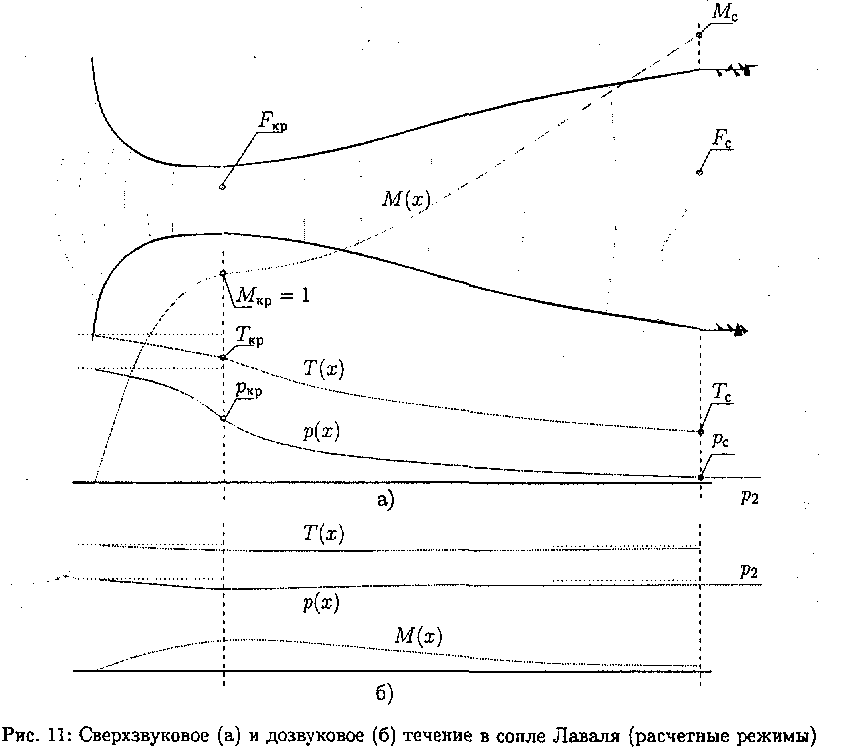
В том же случае, когда в узком сечении сопла Лаваля звуковая скорость не достигается (M < 1), то в последующем расширяющемся участке число M продолжит снижаться и течение по всей длине такого сопла остается дозвуковым (рис. 11.4, б). В идеале стационарное течение в сужающемся участке канала (конфузор) может рассматриваться как обратимый процесс разгона газа, и, соответственно, течение в расширяющемся участке (диффузор) — как обратимый процесс его торможения. В пределе F → ∞ на выходе из такого канала поток, ускоренный в конфузоре, окажется стационарно заторможенным в диффузоре до тех же значений статических T и p, что и на входе в канал, т. е. протекает обратимый процесс. Конечная величина G через такой идеализированный канал получается при бесконечно малом перепаде давления, что не может иметь места в действительности. Реальное течение всегда сопровождается потерями на трение о стенку, и обычно существенна неоднородность распределения параметров по сечению канала, вплоть до отрыва потока от стенок, чему особенно подвержено течение в диффузорах.Поэтому для реальных каналов, сопел, насадков и отверстий не действительный расход газа или жидкости влияют условия на входе и выходе из него, физические свойствами рабочего тела и геометрия канала. Напомним, что учет подвода или отвода тепла по длине канала (отклонения от адиабатности), трения о стенку (путевые потери) и влияния резких перераспределений потока в сечении (потери на местных сопротивлениях) может быть выполнен еще в рамках гидравлического приближения, т. е. может сводиться к применению коэффициентов теплоотдачи, потерь на трение и т. д.
Сверхвуковое сопло. Дальнейшее увеличение M в сопле (канале) после узкого сечения с M = 1 возможно далее при возрастании площади его сечения: dF/dx > 0 (рис. 11.4, а). На этом (сверхзвуковом) участке сопла для определения статических параметров в сечениях идеального сопла также применимы газодинамические функции(ГДФ). Давление на срезе pстакого сопла должно быть меньше критического, и если оно совпадает с давлением в емкости 2, говорят о расчетном режиме течения в сверхзвуковом сопле (сопле Лаваля). При постоянном энергосодержании потока газа (T∗ = const) в сечениях участка dF/dx > 0 при M > 1 увеличивается доля кинетической энергии потока в его энергосодержании и соответственно уменьшается доля энергии теплового движения молекул — снижается статическая температура T.
47. Законы сохранения для стационарных течениях одномерном приближении.
В этом разделе приводится материал, составляющий основу стационарной гидрогазодинамики трубопроводных систем. Стационарное течение описывается здесь в рамках модели, задаваемой уравнениями (законами сохранения) газовой динамики в одномерном (или «каналовом») приближении. При том, что эта модель дает зачастую слишком приближенную картину течения, она полезна в технических приложениях. В расчетах по ней учитываются эмпирические данные, получаемые при более точном (теоретическом или экспериментальном) изучении пространственной структуры потоков. К таким данным относятся,например, зависимости для коэффициентов гидравлических потерь
на местных сопротивлениях или коэффициентов расхода при течении через сопла и отверстия.Материал данного раздела не случайно излагается после изучения основ МЖГ — основных гипотез, вида и способа «замыкания» законов сохранения, описания явлений турбулентности, теорий пристеночного движения, струй и пограничных слоев, что дает возможность критического осмысления условностей и ограничений квазиодномерного
описания.
Стационарное течение в канале. Установившиеся (стационарные)
течения характеризуются независимостью картины течения от времени. Соотношения, справедливые в рамках (квази)одномерного или «каналового» приближения, можно получить, упрощая очевидным образом интегральные уравнения сохранения масс компонентов, импульса и энергии, описывающие течение газовой смеси на гладком1 участке канала.
Соотношения, связывающие параметры потока в сечениях 1 и 2, разделенных конечным расстоянием _x = x2−x1 в этом случае принимают вид:
(ρkuF)2 = (ρkuF)1 , k = 1, . . . K, (11.1)
а эквивалентные им (в подобластях гладкости искомых функций ρk, u, p и т. п.) уравнения в дифференциальной форме (при x2−x1 = dx → 0, а также с заменой _uE + pu на _uh∗), имеют вид:
dGk = d (ρkuF) = 0, k = 1, . . . K, (11.4)
Уравнение количества движения записывается в нетривиальном виде—для его применения следует вычислять интеграл импульса сил на стенке2. Поэтому часто для связи параметров стационарного потока в сечениях 1 и 2 гладкого канала взамен этого уравнения используется связь между давлениями стационарноготорможения p2 и p1,например, следующего вида:
p2 = p1σ(M1, Re1 . . . ), где σ ≤ 1—коэффициент восстановления полного давления—определяемая чаще всего экспериментально функция условий течения и свойств среды и выражающая отношение полного давления в некотором сечении 2 к полному давлению в сечении 1 (сечение 2 ниже по потоку сечения 1).Введение безразмерной величины σ особенно оправдано для потока, энергетически изолированного на участке 1 – 2. Как показано ниже, в этом случае коэффициентом _ полностью и просто определяется приращение энтропии _s = s2 − s1 на участке между сечениями 1 и 2. Таким образом, σ характеризует величину гидравлических потерь на участке (элементе) канала или трубопровода.
К гидравлическим относят потери (полного давления, работоспособности, располагаемой работы), связанные с необратимым превращением части механической составляющей энергии потока в энергию теплового (хаотического) двиижения молекул, т. е., во внутреннюю энергию элементов среды. Реальные течения всегда сопровождаются потерями такого рода, даже в энергетически изолированных («адаиабатных») условиях. Гидравлические потери, как известно, условно подразделяют на путевые потери (потери на трение о стенку; механизм потерь — работа внутреннего трения) и меcтные потери (потери на местных сопротивлениях, вызываемые резким нарушением структуры потока в местах нарушения гладкости профиля канала). В простейшем случае, заменив уравнение количества движения условием постоянства энтропии s2 = s1, придем к идеализированной модели течения в гладком канале—сопле или диффузоре, в расчете которого допустимо пренебречь как теплообменом со стенкой, так и трением.
