1.Научная дисциплина «Механика жидкости и газа». Ее место в системе естественнонаучных знаний.
Объект и предмет изучения в механике жидкости и газа (МЖГ, англ. fluid mechanics, fluid dynamics) механическая форма движения материи как подвижной (текучей) сплошной среды, называемой просто жидкостью — часто называется безотносительно к агрегатному состоянию текучей сплошной среды: газ или смесь газов; термином «капельная» жидкость иногда подчеркивается именно жидкое агрегатное состояние среды.
В качестве фундаментальной или наиболее обшей основы для описания явлений в рамках МЖГ используется закон сохранения (ЗС): массы, количества движения и энергии, помимо которых МЖГ оперирует также соотношениями, характерными для механики, термодинамики, молекулярно-кинетической теории газов.
Место МЖГ как дисциплины в системе естественнонаучных знаний. МЖГ следует рассматривать как раздел механики, и котором моделью рабочего тела является подвижная жидкость; МЖГ является членом иерархии дисциплин, изучающих различные аспекты механической формы движения: механика (динамика) материальной точки, динамика абсолютно твердою тела, динамика деформируемого тела, динамика (механика) идеально деформируемого (текучего) тела — жидкости.
2.Основные гипотезы мжг гипотеза сплошности и гипотеза о локальном термодинамическом равновесии.
Первая из них — гипотеза сплошности нужна, чтобы уйти от необходимости описания индивидуального поведения структурных элементов жидкости. Принимается, что жидкость представляет собой сплошную среду, характеристики которой получаются как статистические средние от характеристик множества структурных элементов. Tак, плотность (объемная плотность массы) р сплошной среды в данной точке определяется осреднением по малому объему в окрестности точки:
где N — количество структурных элементов (молекул) в малом объеме V окрестности точки, тп — масса каждой частицы. Точно так же скорость среды (векторная величина!) в точке определяется осредненным импульсом частиц в малом объеме — через объемную плотность импульса mV:
Гипотеза сплошности верна дли тех задач, в которых наименьший масштаб изучаемых явлений в пространстве и во времени больше минимального масштаба малого объема, содержащего еще достаточно много структурных элементов, чтобы при осреднении не обнаруживалось заметных флуктуации. Оценки показывают, что для гидродинамических явлений в жидкостях и достаточно плотных газах в технике применение гипотезы сплошности вполне обоснованно.
Итак,
осреднение параметров среды но объемам
надлежащего масштаба дает определенные,
кусочно-гладкие (без случайных флуктуаций)
распределении параметров среды. Принятие
гипотезы сплошности в качестве
аксиомы позволяет исключить из
рассмотрения малый объем V
и
приписывать любой токе пространства-времени
вполне определенные значении характеристик
среды — параметров состояния и компонент
скорост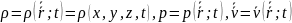и:
и
др., а также сделать «законными» операции,
например, дифференцирования таких
функций
Вторая — гипотеза о локальном термодинамическом равновесии (ЛТР) — позволяет считать, что при любом изменении состояния микрообъема среды в потоке его молекулярная статистика релаксирует достаточно быстро. Это позволяет считать во всех случаях правомерными соотношения, характерные для термодинамически равновесных условий – равновесные распределения молекул по скоростям, а составляющие их энергии – по поступательным, вращательным и колебательным степеням свободы и т.п. в частности, это позволяет вычислять любой зависимый параметр состояния среды(включая коэффициенты молекулярного переноса) по двум независимым параметрам, словом, использовать известные УС во всех точках изучаемого потока среды.