4. 60. Даны значения rss и ess, число наблюдений и число предикторов в регрессии. Проверить гипотезу о качестве модели на основе статистики Фишера.

5. 61. Дано значение r2, число наблюдений и число предикторов в регрессии. Проверить гипотезу о качестве модели на основе статистики Фишера.

Ho : R²= 0 vs H1 : R² не равно 0

для проверки значисмости R² (выборочный) используется специальная статистика Фишера

f(R² ) = F (статистика Фишера)

(**) F= ((ESS/ТSS) *1/k) / ((RSS/TSS) * 1/N-k) = ((1/k-1) * R²)) /(( 1/N-k) * (1- R² ) )

k- число оцениваемых параметров модели (предикаторов)

N – число наблюдений

При верности Ho: F ~ F ( k-1; N-k)

Распределение Фишера (связано с нормальным)

F (k,m) = (1/k * χ² (k)) / (1/m * χ² (m))

χ² (k) = ∑z² , где Z ~ N (0,1) z – это стандартная нормальная величина

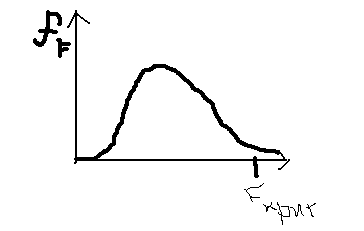
Считаем F по формуле (**), если попало в критическую зону, то R² отличен от нуля

R² =1, если наша регрессионная прямая прошла через все точки, хорошая модель

чем больше R² , тем лучше модель

62. Дан t-статистика, проверить гипотезу с помощью Фишера.

Гипотеза:

Н0: B0=0

H1: B1не равна 0.

Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством

Если t_табл < t_факт, то Hо отклоняется, т.е. а, b и r_xy не случайно от­личаются от нуля н сформировались под влиянием систематически действующего фактора x, Если t_табл > t_факт то гипотеза Нo не откло­няется

63. Дана таблица дисперсионного анализа. Заполнить пропуски в таблице.

Таблица состоит из значений TSS, RSS, ESS.

TSS (Total) = RSS (остатки) + ESS (модель регрессии)

TSS = ∑(y_i – y_{среднее})²

ESS = ∑(y_крышка – y_{среднее})²

RSS = ∑(y_i – y_крышка)²

reg dem_2000 cli gini_ye

64. Дана таблица выдачи регрессионного анализа. Запишите полученное уравнение регрес-сии

Source | SS df MS Number of obs = 25

-------------+------------------------------ F( 2, 22) = 13.86

Model | 6.88491132 2 3.44245566 Prob > F = 0.0001

Residual | 5.46595999 22 .248452727 R-squared = 0.5574

-------------+------------------------------ Adj R-squared = 0.5172

Total | 12.3508713 24 .514619638 Root MSE = .49845

------------------------------------------------------------------------------

dem_2000 | Coef. Std. Err. t P>|t| [95% Conf. Interval]

-------------+----------------------------------------------------------------

cli | .3920828 .0807622 4.85 0.000 .2245922 .5595733

gini_ye | .0022019 .0182327 0.12 0.905 -.0356105 .0400143

_cons | -.7912347 .7457838 -1.06 0.300 -2.337896 .7554263

------------------------------------------------------------------------------

Уравнение регрессии:

dem_2000 = - 0,79 + 0,39*cli + 0,002*gini_ye + ε_i

65,66