
- •2. Дайте определение теоретическому коэффициенту корреляции. Что он показывает? в каком диапазоне меняется?
- •3. Почему на практике исследователь не может вычислить сам теоретический коэффициент корреляции?
- •24. В каком случае применение евклидова расстояния не имеет под собой теоретического основания (хотя может давать разумные результаты)?
- •25. Назовите известные Вам алгоритмы агломерации.
- •26. Даны 4 трехмерных наблюдения. Реализуйте их кластеризацию на основе метода ближнего соседа (дальнего соседа, средней связи) и расстояния Евклида (Манхеттен, Чебышев). Постройте дендрограмму
- •27. Дана дендрограмма. Укажите получившиеся кластеры.
- •29. Объясните, почему при кластеризации необходимо приводить все показатели к единой шкале измерения?
- •34. Кто и почему впервые назвал регрессию регрессией?
- •35. В чем суть метода наименьших квадратов?
- •36. Формализуйте идею метода наименьших квадратов в ситуации парной линейной регрессии (в случае центрированных иксов).
- •37. Выведите мнк-оценки коэффициентов парной линейной регрессии (в случае центрированных иксов).
- •38. Как получить мнк-оценки коэффициентов парной линейной регрессии в обычном случае центрированных иксов?
- •39. Покажите связь между коэффициентом корреляции к.Пирсона и коэффициентом β1 парной линейной регрессии. (См рисунок в контакте)
- •Вопрос 40. Сформулируйте 4 условия Гаусса – Маркова.
- •Вопрос 41. Сформулируйте теорему Гаусса – Маркова
- •1. Несмещенность
- •2. Эффективность
- •47.Что такое автокорреляция остатков? Когда она может возникать в регрессионной модели?
- •48. К каким последствиям для свойств мнк-оценок ведет нарушение каждого из условий Гаусса – Маркова?
- •51.Укажите распределение (и его параметры) мнк-оценок коэффициентов регрессии при выполнении условий Гаусса – Маркова и условия нормальности. (смотри оисунок в контакте)
- •52. Дано значение мнк-оценок коэффициентов парной регрессии. Известно число наблю-дений. Проверьте, значимы ли коэффициенты регрессии.
- •53. Дана таблица результатов регрессионного анализа из некоторой статьи англоязычного политологического журнала. Укажите статистически значимые коэффициенты регрессии.
- •54. Даны несколько пар наблюдений над случайными величинами X и y. Постройте уравне-ние регрессии y на X и проверьте значимость коэффициентов.
- •55. Что такое коэффициент детерминации? Что он показывает?
- •56. Даны значения rss и ess. Найти r(квадрат)
- •57. Дано значение коэффициента корреляции между X и y. Найти r(квадрат)
- •60. Даны значения rss и ess, число наблюдений и число предикторов в регрессии. Проверить гипотезу о качестве модели на основе статистики Фишера.
- •61. Дано значение r2, число наблюдений и число предикторов в регрессии. Проверить гипотезу о качестве модели на основе статистики Фишера.
- •63. Дана таблица дисперсионного анализа. Заполнить пропуски в таблице.
- •64. Дана таблица выдачи регрессионного анализа. Запишите полученное уравнение регрес-сии
- •67. Какова природа проблемы мультиколлинеарности в задачах множественной регрессии?
- •68.К чему ведет мультиколлинеарность?
- •73. Каковы методы выявления автокорреляции в задаче регрессионного анализа?
- •74. В чем состоит проблема эндогенности в задаче регрессии? Каковы последствия эндогенности для мнк-регрессии?
- •75.В чем состоит проблема гетероскедастичности? Из-за чего она возникает и каковы ее по-следствия для мнк-оценок коэффициентов регрессии?
- •76.Опишите не менее 2 методов выявления гетероскедастичности остатков в задаче множе-ственной регрессии.
- •77. Опишите известные Вам методы борьбы с гетероскедастичностью остатков в задаче множественной регрессии.
- •78. Назовите задачи, которые решает метод главных компонент.
- •79. Приведите примеры использования мгк в политологических задачах.
- •90. Назовите оптимальные свойства главных компонент.
- •91. Объясните смысл характеристического уравнения для ковариационной матрицы:
- •94. Чему равен коэффициент корреляции между главными компонентами?
51.Укажите распределение (и его параметры) мнк-оценок коэффициентов регрессии при выполнении условий Гаусса – Маркова и условия нормальности. (смотри оисунок в контакте)
52. Дано значение мнк-оценок коэффициентов парной регрессии. Известно число наблю-дений. Проверьте, значимы ли коэффициенты регрессии.
Коэффициент линейной регрессии считается значимым, если его МНК-оценка отлична от нуля.
53. Дана таблица результатов регрессионного анализа из некоторой статьи англоязычного политологического журнала. Укажите статистически значимые коэффициенты регрессии.
Дано значение показателя и его стандартное отклонение. Необходимо разделить значение на отклонение. Полученное число проверяем на попадание в критическую область. (критические области - 95% - 1.96; 99% - 2.6). То есть, чем больше 1,96 получилось число, тем более значим коэффициент.
Не используем здесь критерий Стьюдента при большом количестве наблюдений, т.к. он сходится к нормальному распределению, то есть к 1,96 и 2,6.
54. Даны несколько пар наблюдений над случайными величинами X и y. Постройте уравне-ние регрессии y на X и проверьте значимость коэффициентов.
а)Чтобы построить уравнение регрессии нужно сначала замутить табличку. Где будут следующие столбцы: xi – xср; (xi – xср)( yi – yср); (xi – xср)2.
Уравнение регрессии имеет вид: yi = a + b(xi – xср) - εi
Где
a
= yср,
в свою очередь b
= 
В итоге должно получиться что-то похожее на yi = 6 + 1,076(xi – xср) - εi . Это и есть уравнение регрессии.
Б) Значимость коэффициента проверяем с помощью критерия Стьюдента (t-распределение).
H0: b=0 vs. H1: b≠0
t-статистика = t(n-1), где n – число наблюдений. (n-1) – значение самого левого столбца в таблице; верхняя строка – доверительный интервал, берём 0,05, то есть будет 95%.
Если наш коэффициент больше числа из таблички, то отвергаем нулевую гипотезу – коэффициент значим.
55. Что такое коэффициент детерминации? Что он показывает?
Коэффициент детерминации (R2)— это квадрат множественного коэффициента корреляции. Коэффицент детерминации показывает долю вариации зависимой переменной, объясненную независимой переменной (какая доля дисперсии зависимой переменной объясняется влиянием независимых переменных).
В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции Пирсона, то есть R2 = r2.
56. Даны значения rss и ess. Найти r(квадрат)
R(квадрат)=ESS/(ESS+RSS)
На всякий случай все формулы связанные со всей этой хренью
ESS+RSS=TSS
R(Квадрат)=1 – (RSS/TSS)
R(Квадрат)=(TSS-RSS)/TSS
R(Квадрат)=ESS/TSS
57. Дано значение коэффициента корреляции между X и y. Найти r(квадрат)
R(квадрат) = [R(X,Y)]^2
То есть нужно просто коэффициент корреляции просто возвести в квадрат:-)
Билет № 58 Дано значение коэффициента корреляции между Yˆ и Y. Найти R2.
Формула для нахождения R2:
 ,
,
где
 ,
,
 .
.
Иными словами просто возводите этот коэффициент в квадрат.
На всякий случай формула коэффициента корреляции между Yˆ и Y:
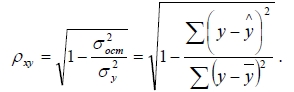
Билет № 59 Дано уравнение парной линейной регрессии. Даны выборочные оценки дисперсии иксов и игреков. Найти R2.
Если использовать выборочную оценку значений соответствующих дисперсий, то получим формулу для выборочного коэффициента детерминации (который обычно и подразумевается под коэффициентом детерминации):

![]() ,
,
![]() ,
т.к.
TSS
=
ESS
+
RSS
,
т.к.
TSS
=
ESS
+
RSS
R SS
=
SS
=![]()
TSS=
![]()
ESS
=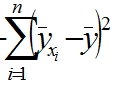
TSS - Total Sum of Squares - полная сумма квадратов
ESS - Explained Sum of Squares - - «объясненная» сумма квадратов
RSS - Residual Sum of Squares - «оставшаяся» сумма квадратов
TSS= RSS+ ESS
или
![]() =
=![]()
![]()
или
![]()
Тогда выражение для коэффициента детерминации можно представить в виде:


