35. В чем суть метода наименьших квадратов?

МНК— один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.

Сущность:

Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов. Геометр. смысл. МНК - это ортогональн. проецир. игрека на икс.

36. Формализуйте идею метода наименьших квадратов в ситуации парной линейной регрессии (в случае центрированных иксов).

Центрирование переменных состоит в параллельном переносе системы координат по Х и/или по Y, при котором наклон (то есть ) не меняется, но упрощается нахождение этого коэффициента. При центрировании Y, дополнительно, свободный член = 0.

Центрированный X = ; EX = 0.

Формализация:

x₁, x₂ … x_n – независимые переменные (регрессоры/предикторы)

y₁, y₂ … y_n – зависимые переменные (отклики)

- общая форма парной линейной регрессии (в обычном случае), где - объясненная моделью часть, а - стандартные ошибки (та часть переменной, которую не удалось объяснить моделью). Построить регрессионную модель = оценить коэффициенты и .

В случае центрированных X мы меняем X на =>

37. Выведите мнк-оценки коэффициентов парной линейной регрессии (в случае центрированных иксов).

Для центрированных X: .

и = 0 => сокращаем.

38. Как получить мнк-оценки коэффициентов парной линейной регрессии в обычном случае центрированных иксов?

Пусть x_i, y_i – исходные данные, а ; - центрированные X и Y.

Для центрированных X и Y:

Тогда для исходных данных:

Выведение МНК-оценок парной линейной регрессии в общем случае (то, что было на лекции):

• | : n (разделим на n)

Подставим во второе уравнение:

; ; => подставим:

| * n

; => заменим:

39. Покажите связь между коэффициентом корреляции к.Пирсона и коэффициентом β1 парной линейной регрессии. (См рисунок в контакте)

Вопрос 40. Сформулируйте 4 условия Гаусса – Маркова.

1)E(ε1) = E(ε2) = … = E(εn) = 0, (15)

2)Var(ε1) = Var(ε2) = … = Var(εn) =  σ2(16) - D(E/x) = сигма в квадрате - условная гомоскедастичность

3)Cov(xi,εj) = 0 при всех значениях i и j (18) -отсутствие эндогенности в узком смысле; распределение Е не зависит от распределения Х

4)Cov(εi, εj) = 0 при i≠j(17)

Единственно-должна отсутствовать автокорреляция

Вопрос 41. Сформулируйте теорему Гаусса – Маркова

Пусть матрица Х коэффициентов уравнений наблюдений (6) имеет полный ранг, а случайные возмущения (8) удовлетворяют четырем условиям,

В этом случае справедливы следующие утверждения:

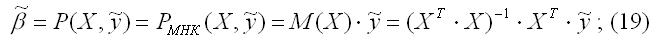а) наилучшая линейная процедура (13), приводящая к несмещенной и эффективной оценке (11), имеет вид:

б) линейная несмещенная эффективная оценка (19) обладает свойством наименьших квадратов:

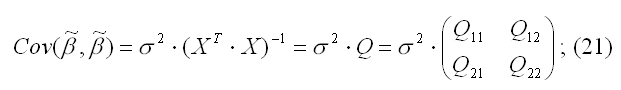
в) ковариационная матрица оценки (19) вычисляется по правилу:

г) несмещенная оценка параметра σ2 модели (2) находится по формуле:

Короче говоря, если выполняются 4 условия Гауса-Маркова, то МНК оценки являются несмещенными, состоятельными и наиб. Эффективными среди всех линейных оценок.

Свойства точечных оценок