1. Рассмотрите любые 3 показателя социальной, политической или экономической статистики и покажите, что каждый из них следует рассматривать как случайную величину. Приведите примеры не менее 3 случайных факторов, влияющих на каждый из рассматриваемых показателей.

- Измеренный уровень ВВП. Он является случайной величиной, т.к. вычисляется на основе огромного множества факторов, которые мы не в силах полностью описать. Случайные факторы: природные катаклизмы (может быть нарушено производство); наличие теневой экономики (ее невозможно точно измерить); погрешности измерения.

- Показатель уровня брака на каком-либо заводе. Случайные факторы: технические ошибки в работе оборудования; технические ошибки в работе персонала; ошибки, непредвиденные ситуации на производстве.

- Прогноз исхода выборов, полученный в результате проведения exit poll’a. Случайные факторы: отказ граждан отвечать на вопрос; предоставление заведомо ложных ответов интервьюеру; ошибки в сборе информации, допущенные самим интервьюерами.

2. Дайте определение теоретическому коэффициенту корреляции. Что он показывает? в каком диапазоне меняется?

Теоретический коэффициент корреляции – показатель, характеризующий силу взаимосвязи каких-либо двух выбранных показателей. Показывает взаимосвязь, варьируется от 1 до -1.

Корреляция — это статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой Корреляции двух случайных величин служит коэффициент Корреляции

3. Почему на практике исследователь не может вычислить сам теоретический коэффициент корреляции?

Теоретический коэффициент корреляции – показатель, характеризующий генеральную совокупность. В своей работе исследователь имеет дело только с выборочным коэффициентом корреляции. Иными словами, исследователь можно измерить коэффициент корреляции для выборки, но не для генеральной совокупности.

4. Формула коэффициента корреляции Пирсона.(+применение по предоставленным данным)

где   – выборочные средние.

5. Что показывает коэффициент корреляции Пирсона?

Коэффициент корреляции Пирсона показывает функциональную связь между двумя парными показателями.

Он показывает наличие линейной зависимости между двумя заданными показателями и степень этой зависимости.

Так, если R=1 по модулю, то x и y линейно зависимы.

Если R=0, то х и у линейно независимы.

6. Пусть коэффициент корреляции Пирсона равен 1 – что из этого следует? А если он равен -1?

Если коэффициент корреляции Пирсона равен 1, то исследуемые показатели находятся в прямой линейной зависимости.

Если коэффициент корреляции Пирсона равен -1, то исследуемые показатели находится в обратной линейной зависимости.

7. Пусть коэффициент корреляции Пирсона равен 0,5 – что это значит?

Если коэффициент корреляции Пирсона равен 0,5, то взаимосвязь между объектами может быть описана линейной функцией виде у = 0,5х + b.

8. Назовите не менее двух недостатков коэффициента корреляции Пирсона.

- Коэффициент корреляции Пирсона чувствителен к выбросам

- Коэффициент корреляции Пирсона предназначен для выявления линейной взаимосвязи и может давать искаженные результаты, когда взаимосвязь объектов нелинейна.

9. Формула коэффициента ранговой корреляции Спирмена. (+применение по предоставленным данным)

, где S = . R_i и M_i – ранги наблюдений в первой и второй выборке.

10. Что показывает коэффициент корреляции Спирмена?

Коэффициент корреляции Спирмена показывает степень тесноты связи между ранжировками Х = (х₁, х₂, х₃, …, х_n) и У = (у₁, у₂, у₃, …, у_n). Он позволяет узнать, существует ли ранговая связь между парными значениями исследуемых переменных. Или, иными словами, он позволяет проверить ранжировки на монотонность.

11. Пусть коэффициент корреляции Спирмена равен 1 – что из этого следует? А если он равен -1?

Если коэффициент корреляции Спирмена равен 1, то между объектами наблюдается положительная монотонная взаимосвязь.

Если коэффициент корреляции Спирмена равен -1, то между объектами наблюдается отрицательная монотонная взаимосвязь.

12. Пусть коэффициент корреляции Спирмена равен 0,5 – что это значит?

Если коэффициент корреляции Спирмена равен 0,5, то между объектами наблюдается некоторая положительная монотонная взаимосвязь.

13. Назовите преимущества и недостатки коэффициента корреляции Спирмена по сравнению с коэффициентом корреляции Пирсона.

Преимущества коэффициента корреляции Спирмена:

- высокая робастность (устойчивость к нетипичным наблюдениям)

- широкая область применения

Недостатки коэффициента корреляции Спирмена:

- не показывает конкретную функциональную связь между двумя переменными

- по большему счету подходит только для фиксации монотонной связи

14. Пусть на основе эмпирических данных вы получили, что R = 0,15 (это коэффициент корреляции Пирсона). Требуется понять, можно ли на основании этого результата утверждать, что на самом деле есть корреляция между иском и игреком. Как это сделать? Дайте ответ, если число наблюдений n = 25.

Решение:

1. H₀: Corr (X,Y) = 0 vs. H₁: Corr (X,Y) 0

2. 

3. t_(n-2)

4. Считаем и подставляем в формулу. Потом смотрим по распределению Стьюдента.

15. Пусть на основе эмпирических данных вы получили, что р = 0,15 (где р = коэффициент корреляции Спирмена). Требуется понять, можно ли на основании этого результата утверждать, что на самом деле есть корреляция между иксом и игреком. Как это сделать? n = 25.

Решение:

1. H₀: Corr (X,Y) = 0 vs. H₁: Corr (X,Y) 0

2. 

3. 

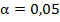
4. Считаем и смотрим ответ. Если он лежит в интервале от -1,96 до 1,96, то H₀ верна.

16. Для решения какой задачи применяется кластерный анализ?

Кластерный анализ решает задачу разбиения заданной выборки объектов на подмножества-кластеры таким образом, чтобы каждый кластер состоял из схожих объектов, а объекты из разных кластеров имели между собой как можно более существенные отличия. Главная цель – нахождение групп схожих объектов в выборке.

17. Укажите информацию, требующуюся исследователю «на входе» для решения задачи кластеризации.

1. Массив р-мерных наблюдений.

2. Априорные представления о классах.

3. Ожидаемые размеры и число кластеров.

18. Укажите, что является результатом кластеризации (что получается «на выходе»).

На «выходе» мы имеем правило классификации, позволяющее наилучшим в определенном смысле образом разбить имеющиеся р-мерные наблюдения на однородные в определенном смысле группы.

19. Какие виды кластерного анализа вам известны?

Иерархические (делятся на агломерационные и дивизивные) и неиерархические.

20. Как называется графические отражения алгоритма иерархической кластеризации?

1. Дендрограмма

2. Icicle plot (вертикальный и горизонтальный варианты).

21. Сформулируйте свойства, которым должно удовлетворять любое расстояние. Какое из этих свойств выполняется не всегда (например, в психологических исследованиях)?

1) d (O i , O j ) > = 0 2) d (O i ,  O i ) = 0 3) d ( O i , O j )  = 4*) d ( O i , O j )= d ( O j , O i )

Три свойства расстояния

1. Расстояние всегда положительно.

2. Сумма расстояний от a до b и от b до c равна расстоянию от a до c.

3. Расстояние от a до b равно расстоянию от b до a. (выполняется не всегда)

22. Какие виды метрики (расстояний) Вам известны?

1. Расстояние Евклида

2. Расстояние Манхеттена

3. Расстояние Чебышева

4. Квадрат расстояния Евклида

23. Даны 2 четырехмерных наблюдения (2 точки в четырехмерном пространстве). Вычислите между ними расстояния: Евклида, Манхеттен, Чебышёва.

Расстояние Евклида: dist =

Расстояние Манхеттен: dist =

Расстояние Чебышева: dist = Max

Q1 = x₁⁽¹⁾ Q2 = x₂⁽¹⁾

x₁⁽²⁾ x₂⁽²⁾

x₁⁽³⁾ x₂⁽³⁾

x₁⁽⁴⁾ x₂⁽⁴⁾

1. Расстояние Евклида:

d^ев=√ (x₁⁽¹⁾ -x₂⁽¹⁾)² + (x₁⁽²⁾ -x₂⁽²⁾)² +(x₁⁽³⁾ -x₂⁽³⁾)² +(x₁⁽⁴⁾ -x₂⁽⁴⁾)² (все под корнем)

2. Расстояние Манхетен

d^ман= ∣x₁⁽¹⁾ -x₂⁽¹⁾∣ + ∣x₁⁽²⁾ -x₂⁽²⁾∣+ ∣x₁⁽³⁾ -x₂⁽³⁾∣+ ∣x₁⁽⁴⁾ -x₂⁽⁴⁾∣

3. Расстояние Чебышёва

d^чеб= max ⎨∣x₁⁽¹⁾ -x₂⁽¹⁾∣ + ∣x₁⁽²⁾ -x₂⁽²⁾∣+ ∣x₁⁽³⁾ -x₂⁽³⁾∣+ ∣x₁⁽⁴⁾ -x₂⁽⁴⁾∣⎬(из всех разностей выбирается наибольшая, которая и является расстоянием)