8.2 Физический и математический маятники

Физический маятник/ФМ/. ФМ представляет собой некоторое физическое тело, подвешенное в точке, не совпадающей с центром тяжести /масс/. Если ось предполагаемых колебаний проходит через центр масс данного тела, то не выполняются два основных признака колебательной системы: наличие положения равновесия и возвращающей силы.

Пусть фМ колеблется вокруг горизонтальной оси, проходящей через точку 0 /см. рис./ К центру тяжести приложена сила тяжести. В данном случае положение равновесия достигается при совпадении отрезка ОС с вертикалью, будет действовать возвращающий момент сил:

Знак " - " обусловлен тем, что

M_вз< 0, если >0 и

М_вз > 0, если <0

На основании основного закона

динамики вращательного движения можем записать:

или, при малых

В развернутом виде:

Поделив на  будем иметь:

Введем обозначение , перепишем /1/ в виде

Мы получили дифференциальное уравнение свободных незатухающих колебаний, решением которого, как мы знаем, будет функция:

Таким образом, при малых углах отклонения  колебания физического маятника будут носить гармонический характер. При этом частота свободных незатухающих колебаний и период колебаний равны:

Частным случаем ФМ является математический маятник /ММ/ см. рис.

ММ - материальная точка, подвешенная на нерастяжимой и невесомой нити. Теория ФМ охватывает и случай ММ, хотя в данном случае принято рассматривать не изменение угла /формула /3/, а смещение материальной точки из положения равновесия x.

Т.к. ,то

Подставляя выражение для момента инерции материальной точки в формулу /4/ ,получим:

Т.е. период колебаний ММ не зависит от массы m, он определяется значениями длины маятника и ускорения свободного падения.

Введем понятие приведенной длины физического маятника. Приведенная длина физического маятника - это длина такого математического маятника, который имеет тот же период колебаний. В соответствии с определением сравним

откуда следует

8.3 Затухающие колебания,

Мы сделаем существенное приближение к действительности, если учтем наличие силы сопротивления /трения/ F_тр, т.е. учтем диссипадию энергии колебательной системы. Предположим, что сила трения обусловлена внутренним трением в результате движения тела в вязкой среде. См. рис. Тогда будем иметь

Введем обозначение тогда

Мы получили дифференциальное уравнение затухающих колебаний, решением которого является:

,

где

Проверить это утверждение можно путем подстановки /3/ в /2/.  - носит название коэффициента затухания, []=c^-1. Если - время убывания амплитуды вдвое, то

Или ; откуда /4/

Затухание колебаний характеризуется логарифмическим декрементом

затухания . Логарифмический декремент затухания - это величина, численно равная натуральному логарифму отношения двух последующих амплитуд, т.е.

/5/

Отметим, что на практике ₀, поэтому можно считать

На графике затухающие колебания имеют вид, показанный на рис.

Огибающая кривая представляет собой зависимость амплитуды от времени:

8.4 Вынужденные колебания. Резонанс.

Рассмотрим колебательную систему - груз, присоединений к пружине /см. рис. /. Пусть на груз действует гармоническая сила:

/1/

Эта сила называется вынуждающей. Частота ее изменения -, амплитуда - . С учетом вынуждающей силы можем записать:

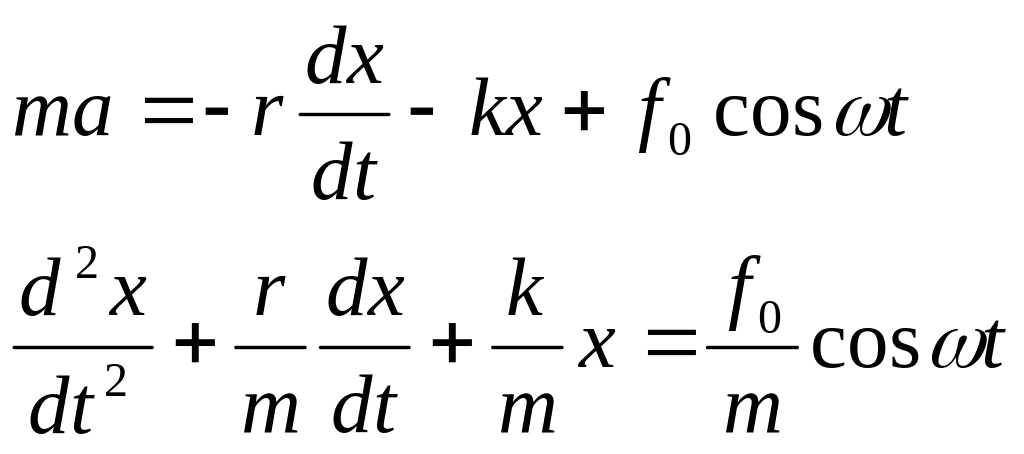
Применяя введенные ранее обозначения, получим

Рассмотрим уравнение /2/ в простом случае, когда -

/3/

Естественно предположить,

что с течением времени тело будет совершать гармонические колебания с частотой вынуждающей силы , т.е.

/4/

причем , т.к. . после подстановки /4/ в /3/:

откуда

При амплитуда вынужденных колебаний стремиться к бесконечности. Однако, в действительности амплитуда возрастает, но остается конечной, т.к. существует диссипация энергии.

На рис. показана зависимость

амплитуды вынужденных колебаний x₀ от частоты изменения вынуждающей силы . Решая дифференциальное уравнение /2/, учитывающее затухание, можно получить следующую зависимость

/5/

Именно эта зависимость представлена на данном рис. графиче­ски. Исследование функции на экстремум, можно осуществить исследуя на экстремум подкоренное выражение в формуле /5/; Для чего приравняем производную нулю: ;

/6/

Частота вынуждающей силы, при которой амплитуда колебаний системы достигает максимума, называется резонансной . Из /6/ :

Таким образом, можно записать

При совпадении частоты изменения вынуждающей силы с частотой

резонансных колебаний системы амплитуда колебаний достигает максимальных значений. Подставляя в формулу /5/ выражение резонансной частоты, находим максимальное значение амплитуды колебаний:

/8/

Амплитуда резонансных колебаний тем больше, чем меньше коэффициент затухания и чем больше амплитуда вынуждающей силы, Представляют интерес два предельных случая: случай очень низких частот

и случай очень высоких частот изменения вынуждающей силы. Переходя к соответствующему пределу в формуле /5/ , мы получим на низких частотах

т.е. выполняется закон Гука;

на высоких частотах ; ; т.е. результате преобладания сил инерции смещение тела из положения равновесия убывает.

Примеры проявления резонанса колебаний привести самостоятельно.