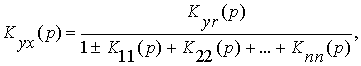1.4.1. Типовые звенья

Чем подробнее математическая модель САУ, тем выше порядокn ее дифференциального уравнения. Передаточные функции систем высокого порядка (обычно n > 4) оказываются громоздкими и неудобными для анализа. Чтобы выйти из этого положения, передаточную функцию представляют в виде произведения простых сомножителей, порядок которых не превышает двух. Такие сомножители называют типовыми звеньями.

Звенья одного типа описываются одинаковыми дифференциальными уравнениями (уравнениями динамики), определяющими характер переходных процессов, которые возникают в них. Уравнение динамики (системы) – это уравнение, определяющее зависимость выходной величины элемента (звена) y(t) от входной величины x(t):

.

Уравнение динамики может быть записано в дифференциальной и операционной форме.

Дело упрощается еще и тем, что при нахождении передаточных функций отдельных элементов системы они обычно сразу выражаются через типовые звенья. В этом мы убедимся на конкретных примерах, которые рассматриваются ниже. Число комбинаций типовых звеньев ограничено. Различают семь основных типов со своими передаточными функциями:

усилительное звено

K_y(p)'= k;

интегрирующее звено

;

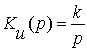апериодическое звено

;

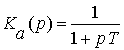колебательное звено

;

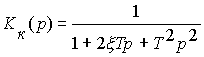идеальное дифференцирующее звено

;

дифференцирующее звено первого порядка

K_д1(p) = 1+ pT

и дифференцирующее звено второго порядка

K_д2(p) = 1+2x Tp+T²p^p.

Усилительное звено является безинерционным; интегрирующее, апериодическое и колебательное образуют группу инерционных звеньев; дифференцирующие объединяются в группу форсирующих звеньев. В выражениях для передаточных функций типовых звеньев постоянныеkназываются коэффициентами преобразования; Т – постоянными времени, а x - коэффициентами демпфирования.

 

1.4.2. Структурные схемы и передаточные функции сау

Для нахождения различных передаточных функций составляют структурную схему системы. В основе ее лежит функциональная схема, в которой каждый элемент заменяется его передаточной функцией. Передаточные функции нескольких элементов могут группироваться или, наоборот, расчленяться на большее число составляющих в зависимости от удобства исследования.

В результате структурная схема оказывается состоящей из ряда звеньев. Каждое звено структурной схемы не обязательно соответствует определенному элементу функциональной схемы, а может быть либо его частью, либо соответствовать соединению нескольких элементов. Структурные схемы в зависимости от решаемой задачи могут преобразовываться от одной формы к другой с полным сохранением всех исходных свойств. Подобные эквивалентные преобразования будем называть структурными.

Первоначально условимся о некоторых обозначениях. Звено на структурной схеме изображается, как показано на рис. 13, а, с указанием направлений входа, выхода и передаточной функции. Для систем, работающих по способу отклонения, используют специальное обозначение для измерителя рассогласования, которое показано на рис. 13, б. Кружком отображается операция алгебраического сложения двух сигналов.

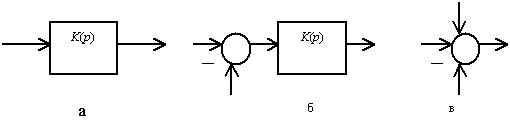
Рис. 13. Изображение звеньев структурной схемы: а – изображение звена; б – изображение измерителя рассогласования;  в – изображение сумматора 

Для сигнала с отрицательным входом используют знак “ - ”, а для сигнала с положительным входом знак не указывается. Звено алгебраического сложения называется сумматором. С помощью подобного звена показывают и наличие других воздействий, которые суммируются с сигналами внутри системы. Схематически подобная операция показана на рис. 13, в. Указанные звенья являются составными частями структурной схемы. Для примера на рис. 14показана структурная схема системы управления антенной. Здесь черезK_п(p), K_у(p), K_д(p),K_тг(p) обозначены передаточные функции элементов: измерительного, усилительного, двигателя и тахогенератора. Кроме того, для примера изображены возмущающие воздействияv₁(t) и v₂(t), приложенные на входе и внутри системы.

На структурной схеме элементы могут соединяться последовательно, параллельно и в виде соединения с обратной связью. Надо иметь в виду, что в замкнутых САУ с работой по сигналу рассогласования, в цепи обратной связи на сумматор измерителя рассогласования подается сигнал с отрицательным знаком. Так, сигналy(t) на первом сумматоре (рис. 14) имеет знак “ - ”.

По этой причине системы, работающие по способу отклонения, называют системами с отрицательной обратной связью. Внутренние контуры многоконтурных САУ могут иметь как отрицательные, так и положительные обратные связи.

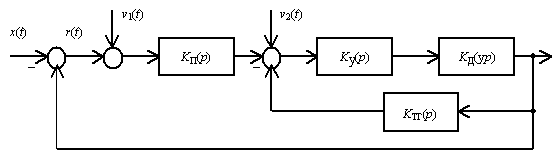
Рис. 14. Структурная схема системы управления антенной

Для осуществления структурных преобразований надо знать несколько правил нахождения передаточных функций.

Вначале рассмотрим правило для последовательного соединения (рис. 15, а). Для этого соединения справедливы равенства

y(p) = y₁(p)K₂(p) и y₁(p) = x(p)K₁(p)

и передаточная функция последовательного соединения

.

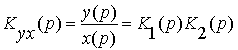На рис. 15, б изображено параллельное соединение звеньев. Их выходные сигналыy₁(t) иy₂(t) алгебраически складываются, что условно показано знаками “ ± ” на схеме.

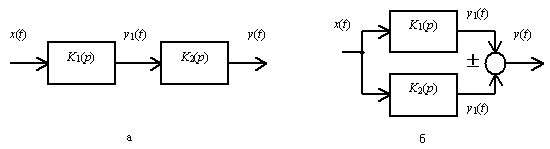
Рис. 15. Последовательное (а) и параллельное (б) соединение звеньев

В результате изображение выходного процесса

y(p) = ± y₁(p) ± y₂(p).

Так как

y₁(p) = x(p)K₁(p);

y₂(p) = x(p)K₂(p),

то

y(p) = x(p)[ ± K₁(p) ± K₂(p)] ,

откуда передаточная функция параллельного соединения

(8)

Рассмотрим соединение с обратной связью (рис. 16). Знаками “ ± ” отмечено, что обратная связь в такой схеме может быть как положительной (знак “ + ” ), так и отрицательной (знак “ - ”). Запишем следующие очевидные равенства:

y(p) = r(p)K₁(p);

r(p) = x(p) ± y_ос(p);

y_ос(p) = y(p)K₂(p).

Подставляя переменные последовательно друг в друга, начиная с последнего, получим

y(p) = [ x(p) ± y(p)K₂(p)] K₁(p) = x(p)K₁(p) ± y(p)K₁(p)K₂(p).

Группируя подобные члены, получим равенство

.

Заметим, что в левой части порядок знаков поменялся на противоположный. Теперь положительной обратной связи соответствует знак “ – ”, а отрицательной соответствует знак  “+”.  Передаточная функция соединения с обратной связью

.

(9)

Пример.

В качестве примера использования этих правил, рассмотрим структурные преобразования для схемы системы управления антенной (рис. 14). Если звенья К_д(р) и К_тг(р), образующие соединение с отрицательной обратной связью, заменить одним звеном с передаточной функцией

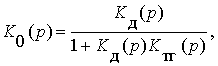
то придем к структурной схеме (рис. 16, а).

Объединим три последовательно соединенных звена К_и(р),К_у(р) и К_о(р)

в одно с передаточной функцией

В итоге получим структурную схему, показанную на рис. 16, б.

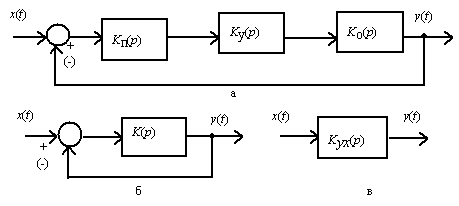
Рис. 16. Структурное преобразование исходной схемы (а) в соединение с обратной связью (б) и в итоговую схему (в)

И, наконец, эту схему можно заменить одним звеном с передаточной функцией

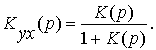
Таким образом, мы получили несколько структурных схем различной сложности, соответствующих одной и той же системе. В самом простейшем случае система может быть представлена одним звеном с соответствующей передаточной функцией, как это имеет место на рис. 16, в.

 

Пример.

Выведенные правила можно использовать для нахождения передаточных функций по различным воздействиям. Покажем это на примере. Вновь обратимся к рис. 14 и найдем передаточную функцию

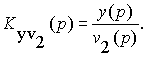
По отношению к этому воздействию звенья К_у(р),К_д(р) и К_тг(р) будут находиться в прямой цепи, а звено К_п(р) – в цепи обратной связи.

Передаточная функция для прямой цепи

,

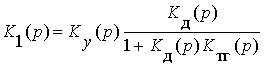где учтено соединение с обратной связью звеньев К_д(р) и К_тг(р) и последовательное соединение с ними звена К_у(р).

В итоге по правилу соединения с обратной связью сразу можно записать, что

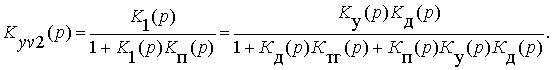
Подобными приемами можно найти и другие интересующие нас передаточные функции. Для решения некоторых задач удобно применять правило нахождения передаточной функции многоконтурной системы (рис. 17).

Последовательно применяя выведенные ранее правила, можно показать, что передаточная функция многоконтурной системы

(10)

где

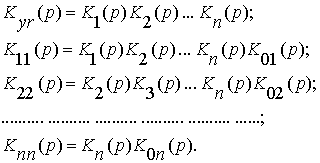
Нижние индексы отражают те процессы, между которыми устанавливает соответствие данная передаточная функция.

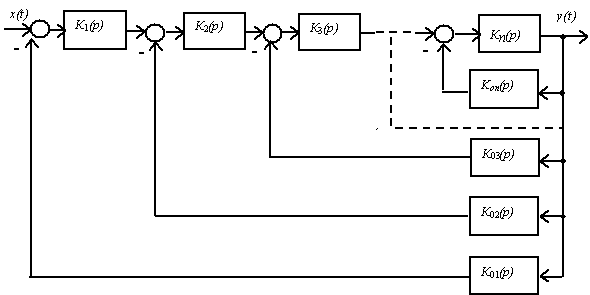
Рис. 17. Структурная схема многоконтурной САУ

Полиномы числителя и знаменателя передаточной функции легко находятся по исходному дифференциальному уравнению

.

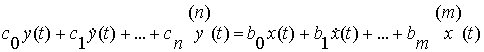Из выражения для передаточной функции замкнутой САУ следует, что передаточная функция является отношением изображений выходного процесса и входного при нулевых начальных условиях.

Передаточные функции могут определяться для различных воздействий в различных точках их приложения и по отношению к различным процессам внутри системы. Так, на рис. 18. показана следящая система с несколькими воздействиями.

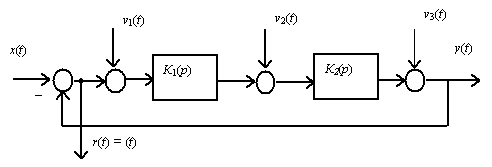
Рис. 18. К определению ошибок в следящих системах

На этом рисунке кроме задающего воздействияx(t) показаны три типа возмущающих воздействий, приложенных на входе системы (воздействиеv₁(t)), внутри системы (воздействиеv₂(t)) и на выходе (воздействиеv₃(t)). Прежде всего, напомним, что в следящей системе

К_и(р) = 1,

а поэтому

у_и(t) = x(t)

и ошибка

e(t) = x(t) – y(t) = r(t).

Таким образом, в следящей системе ошибка управления совпадает с рассогласованием, что и отображено на рис. 18. Перейдем к нахождению передаточных функций ошибок. Для динамической ошибки имеем:

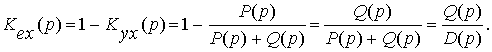
Для возмущающего воздействия, приложенного на входе,

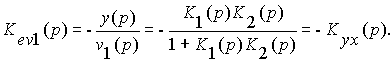
Для второго возмущающего воздействия

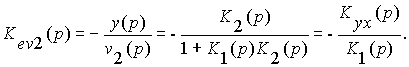
В последнем случае передаточная функция ошибки равна

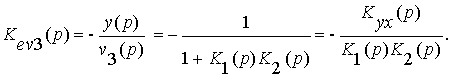
В последних трех случаях при нахождении передаточных функций использованы правила структурных преобразований. Не представляет труда нахождение передаточных функций и для других классов САУ и других видов воздействий.
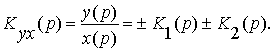
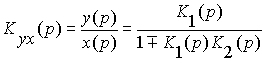