1.2.2. Классификация сау по виду их математических моделей

     Теория автоматического управления имеет дело с математическими моделями, отражающими свойства реальных систем посредством математических соотношений. Всякая математическая модель способна описать систему лишь приближенно с учетом различного рода допущений. На практике стремятся выбрать модель по возможности наиболее простую, что сокращает усилия на ее исследования. Противоречие между простотой модели и степенью ее приближения к оригиналу является обычной трудностью любой теории, в том числе и ТАУ. Непременным требованием при выборе модели считается соответствие изучаемых в ней процессов тем, которые протекают в реальной системе. Если такого соответствия нет, то исследования теряют всякий смысл. Наиболее достоверным признаком пригодности выбранной модели будет сравнение полученных с ее помощью теоретических результатов с результатами экспериментальной проверки реальной системы. В некоторых случаях допустимо сравнение с данными, полученными путем исследования более точных моделей. Таким образом, само понятие модели является условным, зависящим от характера задач и условий их решения. Естественно, что классификация САУ по виду их математических моделей в некотором смысле также будет условной. В самом общем виде математической моделью САУ является оператор преобразования воздействий. Оператором системы называется преобразование, где каждой функции, определяющей закон изменения воздействия, ставят в соответствие другую функцию, определяющую закон изменения выходных координат. Формально это преобразование, например для задающего воздействия, обозначается как

y(t)=x(t)s(t) ,

где s(t) – оператор системы по задающему воздействию. Аналогично определяются и операторы по другим воздействиям. В настоящее время отсутствуют общие методы нахождения операторов желаемой степени сложности и точности для всех классов систем. В этой части большую роль играют опыт и способности исследователя. Однако по ряду частных задач приемы составления математических моделей достаточно хорошо отработаны и экспериментально подтверждена удовлетворительная точность получаемых при этом результатов. Так как теория автоматического управления имеет дело с математическими моделями, то в дальнейшем, упоминая о системах, будем подразумевать, что речь идет об их математических моделях, адекватность которых реальным системам считается доказанной.       В первую очередь системы подразделяются на линейные и нелинейные. Линейной называется такая система, для которой справедлив принцип суперпозиции. Этот принцип для оператора системы записывается следующим образом:

     Все остальные системы относятся к нелинейным. Подобное подразделение имеет практическое значение. Теория линейных систем существенно проще и разработана значительно подробнее, чем теория нелинейных, поэтому при ее составлении модели системы стремятся выбрать ее в классе линейных, что значительно упрощает методику исследования. Конечно, и здесь должно выполняться условие адекватности модели реальным исследуемым явлениям с необходимой степенью точности.       Информация о процессах, протекающих в устройствах системы, передается посредством сигналов различной физической природы: электрических, механических и других. При этом сама информация может быть закодирована в сигналах различным способом. Если все сигналы в системе можно рассматривать как непрерывные, то и сами системы называются непрерывными. Однако в ряде случаев информацию целесообразно передавать с помощью дискретных сигналов, например в виде импульсов напряжения или в цифровом коде, и тогда системы называются дискретными. Часто в одной и той же системе бывают как непрерывные, так и дискретные сигналы. Тогда системы называются дискретно-непрерывными или гиб-ридными.       Если свойства системы с течением времени изменяются и оператор системы s(t) зависит от времени, то системы называются нестационарными, а при неизменных свойствах оператора – стационарными. Основные классы автоматических систем с точки зрения их математических моделей показаны на рис. 10.       Для систем с сосредоточенными параметрами, которые рассматриваются в данной теме, наиболее удобной формой представления операторов являются уравнения. При описании непрерывных систем используются дифференциальные уравнения, а дискретных – разностные уравнения; линейные системы описываются линейными уравнениями, нелинейные – нелинейными; у стационарных систем уравнения имеют постоянные коэффициенты, а у нестационарных – переменные.       В итоге исследование САУ сводится к явному или неявному нахождению решений соответствующих уравнений. С помощью дифференциальных и разностных уравнений удается отразить такие характерные особенности систем, как инерционность и временной характер процессов, протекающих в них. Инерционность выражается в том, что система не может мгновенно реагировать на внезапно приложенное к ней воздействие, а его отработка происходит с некоторым запаздыванием и по форме будет отличаться от исходного воздействия. Инерционные системы называются динамическими, а сама ТАУ является разделом теории динамических систем.       Методы решения уравнений различных классов разработаны неодинаково. Наиболее подробно изучены методы решения линейных уравнений, особенно с постоянными коэффициентами, и значительно меньше разработаны методы решения нелинейных уравнений. Все это однозначно определяет и степень развития различных разделов ТАУ. Так, если теория линейных стационарных систем разработана достаточно полно, то теория нелинейных систем, особенно нестационарных, разработана лишь в отдельных аспектах. Все эти соображения существенно сказываются на методологии изложения ТАУ. 

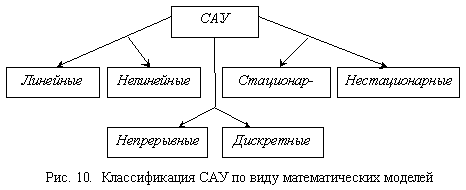
            На практике использование линейных систем часто дает определенные преимущества в качестве управления. Поэтому имеющиеся реальные систе-мы во многих случаях работают в линейном режиме. Все это делает теорию линейных систем фундаментальной частью всей теории автоматического управления.       Таким образом, классификация САУ по виду их математических мо-делей играет особую роль, так как она определяет структуру изложения теории автоматического управления и тем самым влияет на качество усвое-ния учебного материала.