2.2.7. Параметрическая оптимизация

Если структура системы определена, то значение критерия качества будет зависеть от значений ее параметров. Под параметрами системы будем понимать такие величины, как коэффициенты преобразования, постоянные времени и т.п. отдельных ее звеньев. Обозначим эти параметры через

g = g ₁, g ₂, g ₃, ... g _r .

Тогда критерий будет функцией

Q(g ₁,g ₂, ..., g _r) = Q(g ),

где число r определяет количество параметров, которые мы можем изменять. Как правило, влияние параметров на величину Q неоднозначно. При некоторых значениях

g = g _опт

эта величина может принимать экстремальное значение Qэкс. Если характер экстремума согласуется с целью управления, то параметры, при которых он достигается, называются оптимальными. Например, при оценке точности системы по критерию минимума среднего значения функции потерь оптимальными будут те параметры, при которых величина Qдостигает своего минимума

Qэкс = minQ .

Определение оптимальных параметров называется задачей параметрической оптимизации, которая относится к классу вариационных задач. При определении оптимальных параметров обычно приходится сталкиваться с ограничениями, накладываемыми на условия выбора. Простейшим примером таких ограничений может служить требование положительности постоянных времени звеньев. В противном случае задача может потерять физический смысл. При иных условиях могут накладываться ограничения на диапазон выбираемых параметров.

В общем виде ограничения носят характер неравенств

F₁(g ) < N₁; F₂ (g ) < M₂, ..., F_m (g ) < M_m,

где F_i(g ) - некоторые функции от параметров.

Решение задачи параметрической оптимизации с учетом ограничений производится методами математического программирования. Выбор каждого конкретного метода зависит от вида функций Q(g ) и F_i(g ). Если эти функции линейные относительно параметров y, решение ведется методами линейного программирования. Все остальные задачи решаются методами нелинейного программирования. Среди них следует выделить классические методы определения экстремума, градиентные методы, динамическое программирование.

Методы математического программирования являются алгоритмическими. Они не предназначены для получения результатов в явном виде, а дают лишь алгоритмы решения, с помощью которых численными методами могут быть получены искомые оптимальные параметры. Решение в явном виде имеет место лишь в простейших частных случаях.

Если ограничения на выбираемые параметры не накладываются, то для отыскания минимума функции Q(g ) используются необходимые условия существования экстремума.

 

Пример.

Рассмотрим угломерную следящую систему, передаточная функция которой в разомкнутом состоянии имеет вид K(p)=K/p.

Пусть задающее воздействие x(t) будет экспоненциально коррелированным стационарным случайным процессом со спектральной плотностью

 .

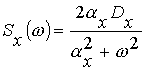Учтем только возмущающее воздействие v(t) от шумов приемника со спектральной плотностью

S_v (w ) = N_v .

Найдем оптимальное значение коэффициента преобразования САУ, обеспечивающее минимум дисперсии ошибки слежения в установившемся режиме.

При статистически независимых воздействиях

D_e = D_ex + D_ev .

Определим дисперсию ошибки от задающего воздействия

D_ex = I[K_x(p) K_ex(p)],

где K_ex(p) - передаточная функция ошибки по задающему воздействию;

K_x(p) - передаточная функция стационарного формирующего фильтра.

Дисперсия ошибки от задающего воздействия

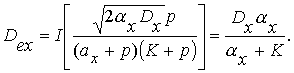
Дисперсия от возмущающего воздействия

 .

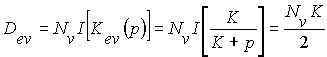Суммарная дисперсия

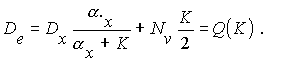
В данной задаче имеется только один оптимизируемый параметр g = K.

Оптимальное значение параметра определим графическим способом.

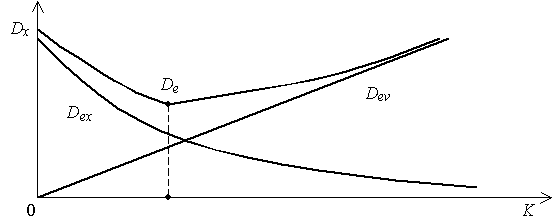
Рис. 62 Дисперсия ошибки в угломерной системе

Это значение соответствует минимуму Q.

При параметрической оптимизации часто используют численные методы, основанные на различных методах поиска экстремума.