2.2.2. Оценка качества переходного режима по переходной

характеристике Переходный режим вызван тем, что система инерционна и должна некоторое время приспосабливаться к поступающим на нее воздействиям. В этих условиях оценку качества удобно вести при наиболее тяжелом с точки зрения воспроизведения системой воздействии, таком, как ступенчатая функция А*l(t). Реакция системы на единичную ступенчатую функцию является переходным процессом h(t), по форме которого в простейшем случае и можно судить о качестве переходного режима.

На рис. 52. изображены переходные характеристики колебательного и монотонного типов, оценка которых проводится с помощью локальных критериев, называемых показателями качества переходной характеристики.

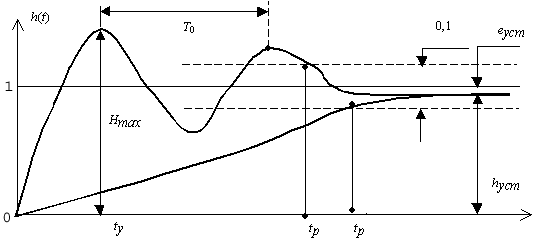
Рис. 52. Показатели качества переходной характеристики

Для характеристик колебательного типа обычно используются следующие показатели: H_m - перерегулирование, которое определяет относительное максимальное отклонение; время установления t_у - момент достижения первого максимума; время регулирования t_р, которое определяет длительность процесса по уровню + 0,05 относительно установившегося значения; период колебаний T.

Для монотонных характеристик наиболее употребительным является показатель длительности переходного процесса t_р. В общем случае точное построение переходных характеристик и, следовательно, определение качества затруднительно. Существует ряд методов, позволяющих приближенно строить переходные характеристики, однако эти методы сложны и приводят к громоздким вычислительным работам. Найти точные значения указанных выше величин удается только для простейших систем первого и второго порядков. Для более сложных следящих систем существуют приближенные формулы их нахождения.

В основе формул лежит знание двух параметров: частоты среза разомкнутой следящей системы w _с  и запаса по фазе.  Эти параметры могут быть найдены аналитически или по логарифмическим частотным характеристикам. Сводка вычислительных соотношений приводится в табл. П. 2.

 

2.2.3. Интегральный квадратичный критерий качества переходного режима

Локальные критерии качества обычно наглядны, но трудно вычисляются аналитически. Примером тому служат показатели переходной характеристики, рассмотренные выше. Интегральные критерии, особенно квадратичные, достаточно легко вычисляются, однако не так наглядны, как локальные. Обратимся к рис.53, на котором изображены два монотонных переходных процесса. Процесс 1 наименьшей длительности. Об этом может свидетельствовать такой косвенный фактор, как площадь между кривой h(t) и уровнем установившегося значения выходного процесса. Отсюда для оценки качества можно ввести критерий

где через e_п (t) обозначена ошибка переходного режима, представляющая разность между текущим и установившемся значениями переходной характеристики. Чем меньше Q, тем выше качество САУ.

Причем подынтегральная квадратичная функция потерь e_п(t) будет неотрицательной как для монотонных, так и для колебательных процессов.

Очевидно, что описанные критерии можно использовать не только для случая переходной характеристики, но и при произвольных воздействиях.

Рис.53. Сравнение качества переходных характеристик

Рассмотрим методику нахождения интегрального квадратичного критерия переходного режима для регулярного воздействия x(t).

Изображение динамической ошибки можно записать в виде произведения

e(p) = x(p)Kех(p)

(29)

Не прибегая к нахождению оригинала e_х(t), можно найти установившееся значение ошибки управления

,

или

.

Если из полной ошибки e_х(t) вычесть ошибку установившегося режима e_х уст, то получим составляющую, которая равна ошибке переходного режима

е_п(t) = e_х (t) - e_х уст.

Очевидно, что

е_п(t)  0 при t    , так как e_х (t)   e_х уст.

Интегральный квадратичный критерий качества переходного режима определим как величину

На основании известной теоремы Парсеваля, нахождение интегрального квадратичного критерия качества Q переходного режима сводится к вычислению интеграла Парсеваля

(30)

Чтобы вычислить конкретное значение этого интеграла, функцию e_п(p) записывают в виде отношения полиномов

.

Тогда интеграл будет функцией параметров a , и  b . Значения функций табулированы и для n< 4 приведены в табл. П.3.

Изображение ошибки переходного режима получаем из формулы:

где учтено, что изображение от постоянной e_x уст равно e _x уст /p.

 

Пример.

Найдем интегральный квадратичный критерий качества переходного процесса в системе управления антенной.

Передаточная функция разомкнутой системы

 ,

Передаточная функция ошибки по задающему воздействию равна

 .

Так как рассматривается переходный процесс, то воздействием является единичная функция

x(t) = 1 (t)

с изображением

x(p)=1/p .

Изображение ошибки управления

.

Установившееся значение ошибки

В итоге получим, что изображение ошибки переходного режима равно

где

a ₀ = 1+K; a ₁ = T; b ₀ = K; b ₁ = 1+K; b ₂ = T.

Согласно формуле (30) интегральный квадратичный критерий качества переходного режима равен интегралу Парсеваля

Q = I [e _п (p)].

Используя данные табл. П.3. для n = 2, находим значение интеграла

 .

Из этого результата видно, что изменением параметров системы можно в широких пределах изменить величину критерия. Особенно характерны в этом отношении два параметра: R и T.

На практике для регулировки показателей переходного процесса широко используют коэффициент преобразования К элемента, не охваченного внутренней обратной связью. В то же время постоянную времени T усилителя следует подбирать так, чтобы величина первого слагаемого критерия не превышала допустимого уровня.