2.1.3. Частотный критерий устойчивости

Наиболее широкое практическое применение для исследования устойчивости систем с обратной связью получил критерий, основанный на рассмотрении частотных характеристик разомкнутых САУ. Этот критерий был предложен в 1932 г. американским ученым Найквистом для расчетов усилителей с обратной связью и носит его имя. Впервые в теорию автоматического управления он был введен советским ученым А.В.Михайловым в 1936 г.

Основные достоинства частотного критерия, обусловившие его широкое распространение:

1. Критерий применим в тех случаях, когда дифференциальные уравнения системы или отдельных ее звеньев неизвестны, но известны частотные характеристики, полученные, например, экспериментально.

2. Использование критерия не так резко усложняется при увеличении порядка характеристического уравнения, как это имеет место при применении алгебраического критерия.

3. Критерий Найквиста еще в большей степени, чем критерий Гурвица, позволяет непосредственно установить влияние на устойчивость системы различных ее звеньев.

4. Критерий дает представление о степени устойчивости системы и показывает возможные пути ее улучшения, если в этом есть необходимость.

5. Критерий позволяет связать исследование устойчивости с последующим анализом качества как в установившемся, так и в переходном режимах.

Частотный критерий Найквиста связывает устойчивость замкнутой САУ с ходом АФХ разомкнутой системы.

АФХ изображается на комплексной плоскости. Для этого комплексная функция K (jw ) представляется в виде ее действительной и мнимой частей.

K(jw ) = ReK(jw ) + jI mK(jw ).

Значения ReK(jw ) и ImK(jw ) откладываются вдоль координатных осей и функция K(jw ) изображается в виде вектора. При изменении w от 0 до   конец вектора описывает на плоскости некоторую кривую (годограф), которая и является АФХ (рис.46)

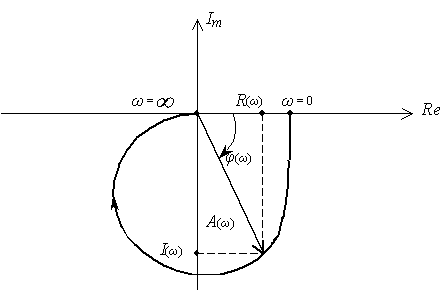
Рис.46. АФХ разомкнутой следящей системы

Критерий Найквиста позволяет судить об устойчивости замкнутой САУ в случаях устойчивой и неустойчивой исходной разомкнутой системы.

Критерий Найквиста для случая, когда разомкнутая система устойчива, формулируется следующим образом: замкнутая система будет устойчивой, если при изменении частоты w от 0до   АФХ устойчивой разомкнутой системы не охватывает точку с координатами - 1, j0.

Для иллюстрации критерия на рис. 47 показаны АФХ устойчивой (а) и неустойчивой (б) систем в разомкнутом состоянии.

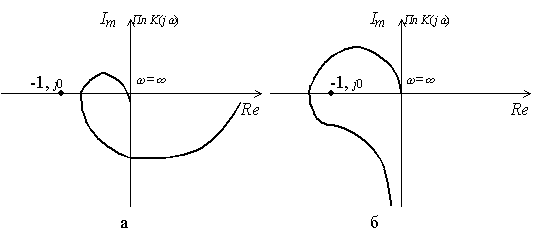
Рис.47. АФХ устойчивой (а) и неустойчивой (б) систем

Таким образом частотный критерий Найквиста позволяет судить об устойчивости замкнутой САУ по виду АФХ исходной разомкнутой САУ (устойчивой или неустойчивой).

 

2.1.4. Логарифмический критерий устойчивости. Запасы устойчивости.

Рассмотрим типовую САУ с единичной обратной связью (рис.48).

Рис.48. Структурная схема типовой САУ с единичной обратной связью

При подаче на вход САУ воздействия вида комплексная гармоническая функция

реакция системы будет также комплексной гармонической функцией

.

Предположим, что при частоте w ^/ комплексная передаточная функция разомкнутой системыK(jw ^/) = -1.

Тогда

т.е. система становится неустойчивой.

Условие K(jw ’) = -1, при котором система теряет устойчивость, может быть записано в виде совокупности условий для амплитудной и фазовой частотных характеристик

A ( w' ) = 1, или L ( w' ) = 0

(27)

/Y (w )/ = 18

(28)

 

Условие (27) получило название условия баланса амплитуд, условие (28) - баланса фаз.

Физически сущность потери устойчивости состоит в том, что входной сигнал передается системой на выход без ослабления, т.к. A(w ) = 1, но с противоположным знаком, т.к. /Y (w )/ = 180° . По цепи обратной связи сигнал y(t) = - x(t) вновь поступает на вход системы с тем же знаком и с той же амплитудой, что и исходный сигнал. В результате ошибка становится равной

E(t) = x(t) - y(t) = 2x(t),

выходной сигнал нарастает, вновь складывается со входным и т.д. до бесконечности.

Рассуждая аналогично, можно показать, что система будет устойчива тогда, когда при выполнении одного из условий - баланса амплитуд или баланса фаз - другое условие нарушается в меньшую сторону, т.е. если

а) при A (w _c) = 1 или L(w _c) = 0:

/Y (w _c)/ < 180° ;

б) при /Y (w  )/ = 180° , A (w ) < 1 или

L (w ) < 0.

Здесь w _c - частота среза разомкнутой САУ, когда A(w _c) = 1, w p - частота, на которой ФЧХ пересекает линию - 180° .

Строгое доказательство частотных критериев устойчивости замкнутых систем было выполнено в 30-х годах советским ученым А.В.Михайловым и американским ученым Г.Найквистом. Наибольшее практическое применение получил критерий, позволяющий оценивать устойчивость замкнутой САУ по логарифмическим частотным характеристикам разомкнутой САУ:

для устойчивости замкнутой САУ при устойчивой разомкнутой САУ необходимо и достаточно, чтобы на интервале частот от w = 0 до w = w _c фазочастотная характеристика разомкнутой САУ не пересекала (или пересекала четное число раз) линию - 180° .

 

Пример.

Передаточная функция разомкнутой САУ

Определить устойчивость САУ по виду частотных характеристик.

Логарифмические частотные характеристики этой системы представлены на рис.49.

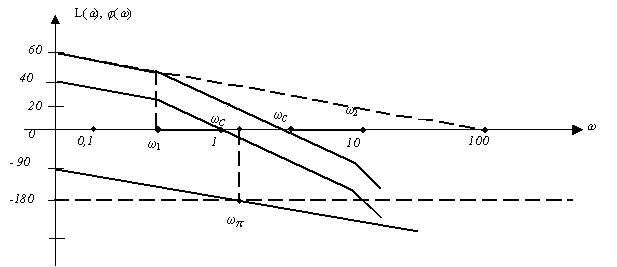
Рис.49. Логарифмические амплитудно-частотная и фазочастотная характеристики

На участке 0 ... w _c ФЧХ пересекает линию - 180° один раз. При этом на частоте среза /Y (w _c)/ > 180° . Следовательно, система неустойчива. Этот же вывод следует из критерия Гурвица, согласно которому предельное значение коэффициента усиления равно

 .

Таким образом, для того, чтобы система была работоспособной, нужно или уменьшать ее коэффициент усиления до K_v < K_{v пред}, или принимать специальные меры - корректировать систему.

При уменьшении коэффициента усиления вид частотных характеристик системы не изменяется, а ЛАЧХ опускается параллельно оси L(w ) вниз.

ЛАЧХ должна быть опущена до такого уровня, когда окажется, что w_c < w  .. Этот признак также является условием устойчивости САУ.