4. Расчётная часть

Для решения поставленной задачи будет использована одна из самых популярных математических систем. Она пользуется большим спросом у студентов, инженеров, экономистов, менеджеров, научных работников и всех тех, чья деятельность связана с количественными методами расчета.

Исходные данные для составления моделей и расчётов помещены в табл. 1 и 2.

Табл. 1

Номер варианта	Периоды времени t	Капитал K (тыс. ед)	Коэффициент ( % от K )
			b1	b2	b3
3	3,4,5,6,7	300	40	35	25

Табл. 2

Периоды времени t	Доходность
	r1(t)	r2(t)	r3(t)	r4(t)	r5(t)	r6(t)
3	0,07	0,15	0,0	-0,1	0,0	-1,5
4	0,14	0,11	0,9	0,3	3,0	1,5
5	0,10	0,10	0,3	0,9	-1,0	2,5
6	0,09	0,14	-0,1	0,5	1,5	1,0
7	0,07	0,05	0,7	0,1	2,5	2,0

Всего рассматривается 6 видов ценных бумаг, то есть N=6. Предполагается, что к 1-ой группе инвестиционного риска относятся бумаги 1-ого и 2-ого видов, то есть J₁={1,2}, ко 2-ой группе – бумаги 3-его и 4-ого видов, то есть J₂={3,4}, к 3-ей группе – бумаги 5-ого и 6-ого видов, то есть J₃={5,6}. Также предполагается, что бумаги 2-ой группы инвестиционного риска (3-его и 4-ого видов) принадлежат к взаимосвязанным областям экономики.

С ледует иметь в виду, что данные о доходности ценных бумаг, приведенные в табл. 2 – гипотетические, то есть не соответствуют реальным ценным бумагам, хотя и отражают характер «поведения бумаг» соответствующего типа.

Величины b_i.i =1,3, указаны в процентах от наличного капитала К.

Расчёт 1-ой модели оптимизации, который предполагает максимизацию ожидаемого дохода при ограничении общего объема инвестиций выглядит так:

Первоначально вводятся все исходные данные и составляется матрица М доходностей по периодам. Далее производится вычисление ожидаемого дохода по каждому виду ценных бумаг.

В следующем шаге записываются условия 1-ой модели оптимизации, после чего используется оператор MathCad Maximize(E,x), который определяет, что максимальный доход при данных условиях 1-ой модели будет при вложении инвестиций в 5-ый вид ценных бумаг.

В следующей части контрольной работы вычисляется 2-ая модель оптимизации, которая предполагает максимизацию ожидаемого дохода при ограничениях, определяемых политикой фирмы.

Первоначально вводятся все исходные данные и составляется матрица М доходностей по периодам. Далее производится вычисление ожидаемого дохода по каждому виду ценных бумаг.

В следующем шаге записываются условия 2-ой модели оптимизации, после чего используется оператор MathCad Maximize(E,x), который определяет, что максимальный доход при данных условиях 2-ой модели будет при вложении инвестиций во 2-ой вид ценных бумаг – 120 тысяч единиц капитала, в 3-ий – 105 тысяч единиц капитала, а в 5-ый – 75 тысяч единиц общего капитала.

В последней части контрольной работы вычисляется 3-ая модель оптимизации, которая предполагает минимизацию инвестиционного риска при заданном среднем доходе.

Первоначально вводятся все исходные данные и составляется матрица М доходностей по периодам. Далее производится вычисление ожидаемого дохода по каждому виду ценных бумаг.

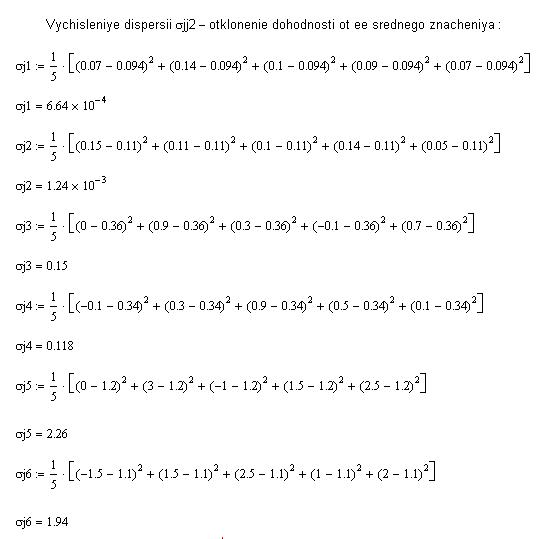
Далее производится вычисление дисперсии по каждому виду ценных бумаг – отклонение доходности от её среднего значения.

Далее производится вычисление ковариации по каждому виду ценных бумаг – оценка инвестиционного риска для пары видов ценных бумаг.

Вычисление инвестиционного риска портфеля ценных бумаг и перечень условий для 3-ей модели оптимизации.

И, наконец, оператор MathCad Minimize(E,x) определяет распределение инвестиций для каждого вида бумаг при заданных условиях 3-ей модели оптимизации.

Таким образом, при ожидаемом доходе E(x*)≥130 тысяч единиц, инвестиционный риск портфеля ценных бумаг V(x*) будет равен 6 198.