1. Скорость , ускорение, перемещение, траектория. Скорость.

при равномерном: v=s/t;

Неравном. дв-е: v^->=ds->/dt; lim _dt->0ds/dt=ds/dt; Направление вектора v, с направлением ds аналогично, т.е. в люб. м. t v направление в сторону дв-я.

V_x=dx/dt; V_y=dy/dt; V_z=dz/dt; a^->=dv^->/dt; v*dt=dx; x=vdt;

1 . v-неизв., ->нет решений 2. V=const, -> x=vdt=vt+x₀ 3. V<>const, a=dv/dt=d²s/dt²; dv=adt; v=adt; a-неизв. ->нет реш. a= const, ->v=adt=at+v0;

X=(v0+at)dt=v0dt+atdt=v₀t+at²/2 =x0

П еремещение – Dr^-> =r — r0, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток t: r+dr-r=dr; ds^->=dr^-> 

Ускорение. a=(a_н²⁺а_т²)^1/2; a_t=dv/dt; a_n=v²/r;

Траектория - линия, вдоль которой движется тело. Длина траектории -  пройденный путь. 

2.Cкорость средняя. Среднее по времени.      Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор r0. В течение малого промежутка времени Dt точка пройдет путь Ds и получит элементарное (бесконечно малое) перемещение dr.      Вектор средней скорости <v> - приращение Dr радиу­с-вектора / dt: Направление <v> совпадает с Dr. 3.Принцип относительности Галилея

Требование: неизменности вида уравнений, выраж. Законы механики при преобразовании координаты t, описыв. Переход из 1 инерц. Системы в др. – преобразования Галилея.

r^->|=-R^->=r^->; r^|=(r²-2rRcosQ+r²)^1/2(1,2)

д опустим К’ движется относительно К c v^->; рассмотрим нек. т. М, предполагая, что покоится в К’. r’=const; вектора r и R-? Можно ли 1,2 – для любого м.t?

Определение r^-> в К’, а r и R в К‘. для измерения r’ –нужна линейка, а r^-> и R^-> движутся, поэтому кроме пространств. Изм-ний нужно с помощью часов, покоящихся в этой с-ме. Одновременно засечь T в координатной сетке К-с-мы.

R^-> и r^-> -различны, Нет утверждений, что 1,2 – справедливо для движ. С-мы К’. Можно только постулировать: выражения 1,2 – справедливы в разных с-х отсчёта, после установки max V=c.

П р.Г. справедливо к в-рам разным СО. Независимо от СО справедливость не ограничивается, пр. М в движ.СО(везде ^->):

r’(t’)=r(t)-R(t); r’(t’)-ф. t’ связанного r’-const dr’(t’)/dt=dr(t)/dt-dR(t)/dt; dr/dt=v^->-k’;dR/dt=V^->

dr’/dt=dr’/dt’-dt’/dt=v^-> - V^->;отсюда в нек. К тело движется с v=сonst, то в -й др. K’ виж. С пост. v отн-но К это тело так же будет двигаться с V’.V^->=const;(R0-пост.в-р)

R(t)=R₀+v(t); r’(t’)=r(t)-R₀-vt; r’=r-R; r’=r-R₀-v;r’=r-vt; t’=; x’=x-v_xt; t’=;

4 . Бегущая волна вывод волнового уравнения. - волны, которые переносят в пространстве энергию. Волновое уравнение. Если в источнике X=Acos(wt+). Колебания в т. на t: x=Acos[w(t-t)+); предпологается, что в процессе распространения не происходит затухания. Плоской в. Синус.: x=Acos[w(t-x/v)+], k=w/v=2/(vT)=2/ - волновое число – сколько единиц волн укладывается на 2, x=Acos(wt-kx+);=>

1.A=const;

2.  фаза т. зависит от удаления от источника колебаний;

3. В нек.м. t: x=Acos(kx+), =-(wt₀+)

Пусть  нек. Возмущение , являющ. Функцией по t. Движение возмущения через v: x=s+(v/t’)*t; Форма возмущения не меняется (x,t)=’+(s); -1; d/dt=df/d; d/dt=f’(-v); d/dx=1; d²/dt²=f’’(v²); d²/dx²=d; - 2; ур.2 описывает только волну, напр. Вдоль оси ох. Для 3 измерений: - уравнение Лапласа; Рассматриваются волны цилиндр., сф., оптич.: ; =0-плоская; 1-цилиндр.;2-сферич;

5.Скорость распространения волн. Скорость звука. Скорость распространения в. – расстояние, кот. проходит за 1 t  т. волновой поверхности. Вектор v направлен по нормали к волновой пов-сти.

В газах зависит от t: v=(R/M*T)^1/2, R-газ. Постоянная, M - Молярная масса; - пост. Для данного физич. В-ва; v=330 м/с; Скорость упругих волн в жидкостях и в тв. Телах превышает скорость звука в газах и зависит от сжимаемости и плотности среды.v=(K/)^1/2 K-модуль объёмной фигуры, - плотность;

Вопрос 6. Сложение гармонических колебаний.

Если система одновременно участвует в нескольких колебательных процессах, то под сложением колебаний понимают нахождение закона, описывающего результирующий колебательный процесс. Рассмотрим сложение двух гармонических колебаний, а именно простейший случай, когда они имеют одно направление и одну частоту ω0:

И спользуем метод векторных диаграмм, рис. 7.7. На данном рисунке х1 и х2 – проекции векторов и на ось ОХ. Поскольку эти векторы вращаются с одинаковой угловой скоростью ω0, то разность фаз - между ними остается постоянной. По правилу векторного сложения (правило параллелограмма) резу льтирующее колебание описывается проекцией вектора на ось ОХ. Уравнение результирующего колебания будет где амплитуда А и начальная фаза φ0 задаются соотношениями:

Сумма двух гармонических колебаний одного направления и одинаковой частоты есть гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания.

Амплитуда результирующего колебания зависит от разности фаз складываемых колебаний:

Вопрос 7.Эффект Доплера для звуковых волн.

П ри движении источника колебаний и приемника (устройства, которое воспринимает звуковые колебания среды) друг относительно друга происходит изменение частоты колебаний, воспринимаемой приемником. Это явление называется эффектом Доплера и имеет место для всех типов волн, включая электромагнитные. В акустике эффект Доплера проявляется как повышение тона при приближении источника звука к приемнику и понижение тона звука при удалении источника от приемника.// Хаббл в 20-х годах 20 в. наблюдая за движениями удаляемых галактик, обнаружил, что они убегают. На основе этого была установлена скорость разбегания галактик.//

Наблюдатель справа заметит большее число волновых гребней, следовательно, частота звука будет выше. С левой стороны волны будут дальше отстоять друг от друга, поскольку автомобиль удаляется от них. Следовательно, за единицу времени мимо наблюдателя, находящегося позади автомобиля, пройдет меньшее количество гребней, и высота звука будет ниже.( d = λ) Пусть источник движется со скоростью v. d _ист. = v*L;Расстояние между гребнями равно длине волны. Если частота колебания источника = ν, то время между двумя испусканиями Т= 1/ν – период. На втором рисунке источник движется со скоростью v . За Т первый гребень пройдет d = v*T, где v – скорость звуковой волны в воздухе. За это же время гребень переместится на d_и = v_и*t. Тогда расстояние между двумя гребнями d′ = d – d_и = (v - v_и)*T = (v - v_и)/ν .| ν′ = v/λ′ = (v*ν)/(v - v_и) | ν′ = . Пусть источник создает звук на высоте 400 Гц и движется со скоростью v=30 м/с; ν′ = = 440 Гц ;

ν″ = – частота для наблюдателя, от которого удаляется автомобиль.

Вопрос 8. Волны. Энергия упругих волн. Вектор Умова.

Волна – любое возмущение, распространяющееся в пространстве: Продольные( , где E – модуль Юнга, – плотность среды) и поперечные( , где G – модуль сдвига).Уравнение волны: x = x₀ cos ω(t - )= x₀ cos(ωt - kx), где k= .||| v= – фазовая скорость. Когда имеется пакет волн(ансамбль близких по частоте) v_гр. = - групповая скорость(характеризует скорость перемещения энергии). Энергия упр волны…ξ = a*cos(w*t-k*x){1} | {2}| Выделим в среде очень маленький объем ΔV такой, что скорость и деформация во всех точках одинаковы. Выделенный объем будет ΔW = 1/2 )². С другой стороны этот же объем имеет и потенциальную энергию упругой деформации U = , где x – относительное удлинение. X= ; E=v² ;W_p = 1/2 )² ; | ΔW_p = 1/2 )² ; | W= ΔW+ ΔW_p = ½* . Продифференцируем выражение {1} по времени и по x: =a*ω*sin(ωt-kx) ; | : =v*a*k*sin(ωt-kx) //k= => ΔW = 1/2 ] = 1/2 ] => . < W_ср.> = ½*ρΔva²ω², т.к. <sin²(_)>=1/2 | | | W=1/2ρa²ω² – плотность энергии. Количество энергии, переносимое волной в единицу времени через некоторую поверхность называют потоком. Φ= или . Плотность потока – это энергия, проходящая через единичную площадь в единицу времени. = . (S= ) So, . = = Wv

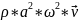= W* = ½ – это выражение носит название вектора Умова