4.3 Свойства экономического объекта (локальные огра­ничения)

В любой, в том числе балансовой модели, для того чтобы охарактеризовать один экономический объект, необхо­димо описать множество различных планов, допустимых для этого объекта. Описать множество планов, допустимых для объекта Р_j можно, указав для каждого количества x_i, произ­водимой этим объектом продукции, какие количества x_1i, x_1i,… x_ni продукции других объектов должны быть поста­влены объекту Р_j. В балансовой модели с этой целью указывается, какие количества продукции других объектов должны быть поставлены объекту Р_j, для того чтобы этот объект мог произвести одну единицу продукции (одну тонну, одну штуку, количество продукции стоимостью в один рубль и т. п.). В соответствии с предположением (2) о комплектно­сти потребления эти количества определяются однозначно.

Обозначим их так:

a_1i, a_2i……a_ni

Числа a_ij носят название технологических коэффициен­тов или коэффициентов прямых затрат. Если их набор известен, то, используя предположе­ние (3) о линейности объектов, легко определить требуемые количества x_1i, x_1i,… x_ni в зависимости от количества произ­водимой продукции x_i из очевидных линейных соотношений:

x _1i= a_1i x_i

…

…

x_ni= a_ni x_i

Пусть теперь известны технологические коэффициенты для всех объектов экономической системы. Эти данные могут быть записаны в виде матрицы nn

A =

i-й столбец который представляет собой набор технологи­ческих коэффициентов объекта Р_j. Матрица А называется матрицей коэффициентов прямых затрат или матрицей технологических коэффициентов. Важной особенностью матрицы А является неотрицательность ее коэффициентов. Это записывается в виде:

A  0

Матрица А технологических коэффициентов содержит всю необходимую информацию для составления системы уравнений балансовой модели.

4.Система уравнений (глобальные ограничения)

Глобальные ограничения балансовой модели представляют собой требование равенства производства каж­дого продукта потребности в нем. Определим потреб­ность в продукции объекта Р_j, если известно, что объем конечной продукции всех объектов описывается вектором:

Y = (y₁, y₂,… y_n)

а полный выпуск продукции всеми объектами — вектором:

X = (x₁, x₂,… x_n)

Для того чтобы некоторый объект Р_j мог выпустить x_i еди­ниц продукции, он должен получить a_ijx_i единиц продукции объекта Р_j Следовательно, для того чтобы был возможен полный выпуск, равный вектору X, все объекты системы должны получить:

единиц продукции объекта Р_j, кроме того, объект Р_j должен выдать в качестве конечного продукта y_i единиц продукции, полная потребность в продукции объекта Р_j, равна:

единиц. Выпуск продукции объектом Р_j равен x_i единиц. Отсюда, для того чтобы был соблюден баланс между выпускаемой объектом Р_j про­дукцией и потребностью в этой продукции, должно выпол­няться следующее балансовое уравнение:

В качестве объекта Р_j мог выступать любой из п объектов, так что имеет место система из п уравнений указанного вида для j = 1,2,…,n.

Система уравнений представляет собой систему уравнений балансовой модели. В векторной форме эту систему можно записать так:

AX+Y=X

В системе уравнений считаются извест­ными матрица технологических коэффициентов А и вектор конечной продукции Y, а вектор полного выпуска X подле­жит определению.

5.Таблица «затраты - выпуск»

Балансовая модель обычно состоит из четырех квадрантов. В первом квадранте дается стоимостная структура отрасли (x_i = v_i + (x_1j + x_2j + … + x_nj), i = 1, 2, …, n). В общей структуре межотраслевого баланса выделяют условно чистую продукцию v_j, к которой относятся амортизационные отчисления, заработная плата, прибыль и т.д.

Во втором квадранте – значения конечной и валовой продукции по отраслям, в третьем – показатели условно чистой и валовой продукции. Четвертый квадрант непосредственного отношения к сфере производства не имеет.

Общий вид таблицы межотраслевого баланса

I квадрант	II квадрант
III квадрант	IV квадрант

Основные соотношения

1. Баланс между производством и потреблением:

x_i = y_i + (x_1j + x_2j + … + x_nj), i = 1, 2, …, n

2. Стоимостная структура продукции в отрасли:

x_i = v_i + (x_1j + x_2j + … + x_nj), i = 1, 2, …, n

3. Равенство между суммарной конечной продукцией и суммарной условно чистой продукцией:

4. Промежуточная продукция экономической системы:

Если все перечисленные выше показатели в тоннах, километрах, штуках и т.д., то таблица называется межотраслевым балансом в натуральном выражении. Однако чаще всего указанные показатели представляются в стоимостном выражении. Необходимо отметить, что планирование только в стоимостных показателях может привести к дисбалансу потоков материально-технического снабжения.

Если под отраслями понимать отдельные производственные подразделения объединения или холдинга указанных подход может быть использован для оптимального планирования этих организаций.

6.Учет факторов производства и поставок из

других экономических систем

Для функционирования отдельных экономических объектов необходимы не только продукция других экономических объектов этой же системы, но такие факторы производства, как производственные фонды (оборудование, производствен­ные площади и т. д.), природные ресурсы (вода, земля, полезные ископаемые, лес и т. д.) и труд; кроме того, экономическая система может получать продукцию других экономических систем (в случае всего народного хозяйства — это импорт из других стран, в случае отрасли или завода — это продукция других отраслей или заводов). Принципиаль­ная особенность как факторов производства, так и поставок из других экономических систем заключается в том, что их количества, которые может использовать экономическая система за некоторый ограниченный промежуток времени, ограничены. Именно ограниченность имеющихся факторов производства и поставок из других экономических систем (факторов) является причиной того, что реально не всякий вектор конеч­ной продукции может быть произведен данной экономичес­кой системой.

Пусть всего таких факторов т. Потребность системы в факторах на период будем обозначать вектором

Z= (z₁, z₂,…,z_n)

где z_i — потребность в i-м факторе; числа z_i могут измеряться как в натуральных единицах (число станко-часов, число кв. метров площади и т. п.), так и в денежных (фонд заработной платы, расходы на закупку импортной продукции и т. п.). Каждый экономический объект P_j будем характеризуется вектором

b_j=( b_1j, b_2j,…,b_mj)

l-я компонента которого указывает, какое количество l-го фактора необходимо объекту P_j, для того чтобы этот объект мог произвести одну единицу продукции; таким образом, предполагается, что объекты обладают свойством ком­плектности потребления и линейности по отношению к фак­торам. Числа b_lj называются коэффициентами прямых затрат факторов. Потребность всех объектов в факторах может быть охарактеризована матрицей коэффициентов пря­мых затрат факторов:

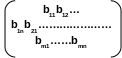
В =

j-и столбец которой состоит из коэффициентов прямых затрат факторов объекта P_j, а l-я строка описывает потребность всех объектов в l-м факторе.

Если вектор полного выпуска продукции объектами системы есть

X = (x₁, x₂,… x_n) ,то суммарная потребность системы в l-м факторе равна:

, (l=1,2,…,m) или

Z = Bx

вектор х является решением системы балансовых уравнении.

7. Применение методов решения систем линейных уравнений

при расчете балансовых моделей

Рассмотрим матричную модель применяемую для отображения соотношения между затратами на производство и его результатами. Например, валовая продукция (полный выпуск) нефтедобывающего предприятия (НДП) составляет 1000 тыс. долл. Валовая продукция или валовой оборот промышленного предприятия – это стоимостной показатель объема промышленного производства, определяемый стоимостью выпуска продукции, работ и услуг всеми производственными цехами за определенный период времени (как правило, за год). При этом используется продукция и услуги собственных подразделений предприятия в объеме $300 тыс. и услуги сервисной фирмы - $250 тыс.

Сервисная фирма имеет следующие показатели: валовая продукция $500 тыс., услуги собственных подразделений $50 тыс. и продукция НДП (так называемый промежуточный продукт) - $100 тыс.

Рис. Схема стоимостных потоков “затраты - выпуск” (в тыс. долл.).

Конечная продукция НДП составляет 1000 - 300 - 100 = $600 тыс. Аналогично конечная продукция сервисной фирмы (услуги на сторону) 500 - 50 - 250 = $200 тыс.

В схеме стрелками обозначены стоимостные потоки, а числами величины этих потоков. Числа в прямоугольниках – валовая продукция для каждой фирмы. Данная модель называется моделью “затраты – выпуск” или моделью межотраслевого баланса. При построении экономико-математической модели удобнее перейти к нормированным величинам, т.е. величинам затрат, отнесенным (в стоимостном отношении) к единице продукции или коэффициентам прямых затрат.