
- •Билет№1
- •Понятие коммутации цепи. Виды коммутации.
- •2. Четырехполюсники. Понятие, классификация. Обратимость четырехполюсников.
- •Классификация четырехполюсников
- •Режим обратного питания четырехполюсников
- •Билет№2
- •1.Причины возникновения переходного процесса.
- •2.Система уравнений четырехполюсника. Понятие симметрии четырехполюсника. Основные уравнения четырехполюсников
- •3.3. Режим обратного питания четырехполюсников
- •Симметричный четырехполюсник
- •Билет№3
- •1.Составление дифференциальных уравнений цепи. Принципы решения дифференциальных уравнений. Классический метод. Классический метод расчета
- •Классический метод расчёта переходных процессов
- •2.Виды соединений нескольких четырехполюсников. Соединения четырехполюсников
- •3.13.1. Каскадное соединение
- •3.13.2. Параллельное соединение
- •3 .11.3. Последовательное соединение
- •Билет№4
- •1.Начальные условия. Законы коммутации.
- •Общая характеристика переходных процессов
- •2.Четырехполюсники в форме ||z|| параметров.
- •Билет№5
- •1.Классический метод расчета переходных процессов.
- •К лассический метод расчета
- •2.Четырехполюсники в форме ||а|| параметров. Условие его обратимости.
- •Определение а–параметров с помощью режимов короткого замыкания и холостого хода
- •Билет№6
- •1.Подключение цепи r,l к источнику энергии. Время переходного процесса.
- •2.Характеристические параметры четырехполюсника: согласованные сопротивления, мера передачи. Характеристические параметры четырехполюсника
- •Билет№7
- •1.Замыкание цепи r,l с накопленной энергией на себя. Время переходного процесса.
- •2.Четырехполюсник в форме ||а|| параметров в гиперболических функциях. Уравнения четырехполюсника в гиперболических функциях
- •Билет№8
- •1.Подключения цепи r,c к источнику энергии. Время переходного процесса.
- •2.Определение параметров эквивалентного четырехполюсника при последовательном, параллельном и каскадном соединении нескольких четырехполюсников.
- •Билет№9
- •1.Замыкание цепи r,c с накопленной энергией на себя. Время переходного процесса.
- •2.Определение параметров эквивалентного четырехполюсника при смешанном соединении нескольких четырехполюсников. . Эквивалентные схемы замещения четырехполюсника
- •Билет№10
- •1.Особенности расчета переходных процессов в цепях второго порядка классическим методом при действительных корнях характеристического уравнения.
- •4.2.6.1. Разряд емкости на цепь rl
- •Билет№11
- •1.Особенности расчета переходных процессов в цепях второго порядка классическим методом при комплексно-сопряженных корнях характеристического уравнения.
- •2.Вторичные параметры четырехполюсника. Примеры их нахождения. Билет№12
- •1.Подключения цепи r,l,c к источнику энергии. Время переходного процесса.
- •Переходные процессы при подключении последовательной r-l-c-цепи к источнику напряжения
- •2.Электрические фильтры понятие и классификация.
- •Билет№13
- •1.Замыкание цепи r,l,c с накопленной энергией на себя. Время переходного процесса.
- •2.Полоса пропускания и полоса задержки электрических фильтров. Граничные частоты пропускания реактивных фильтров.
2.Виды соединений нескольких четырехполюсников. Соединения четырехполюсников
Рассмотрим три вида соединения четырехполюсников – каскадное (цепная схема соединения, рис. 3.8), параллельное (рис. 3.10) и последовательное (рис. 3.11).
3.13.1. Каскадное соединение
Пусть в цепной схеме соединения заданы А–параметры четырехполюсника (АI) и (АII). Выразим напряжение и ток на входе четырехполюсника заданными напряженияими и токами на выходе последнего четырехполюсника (в данном случае второго). Для первого и второго четырехполюсников справедливо
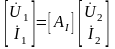 ,
, (3.49)
(3.49)
 .
(3.50)
.
(3.50)
Подставив
значение матрицы
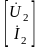 из (3.50) в (3.49), получим
из (3.50) в (3.49), получим
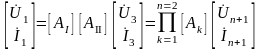 .
.
Если схема состоит из n четырехполюсников, справедливо равенство
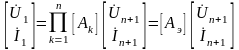 , (3.51)
, (3.51)
где
Aэ
– эквивалентная матрица, равная
произведению n
матриц,
 .
.
Т аким
образом, матрица А–параметров
каскадно соединенных четырехполюсников
равна произведению матриц А–параметров
отдельных четырехполюсников.
аким
образом, матрица А–параметров
каскадно соединенных четырехполюсников
равна произведению матриц А–параметров
отдельных четырехполюсников.
Пусть
имеется два четырехполюсника с постоянными
передачи
 и
и
 и с характеристическими сопротивлениями
и с характеристическими сопротивлениями
 ,
,
 ,
,
 ,
,
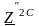 .
Причем,
.
Причем,
 .
Если включить их по цепной схеме (рис.
3.9) и подключить на выходе второго
четырехполюсника
,
то будет иметь место согласованное
включение двух четырехполюсников. В
соответствии с (3.39)
.
Если включить их по цепной схеме (рис.
3.9) и подключить на выходе второго
четырехполюсника
,
то будет иметь место согласованное
включение двух четырехполюсников. В
соответствии с (3.39)
 .
.
После подстановки получим
 .
.
Если цепная схема будет состоять из n согласованных четырехполюсников, то
 , (3.52)
, (3.52)
где
 – напряжение на выходе последнего
четырехполюсника.
– напряжение на выходе последнего
четырехполюсника.
В схеме, состоящей из n согласованных симметричных четырехполюсников
 .
.
3.13.2. Параллельное соединение
П ри
параллельном соединении четырехполюсников
(рис. 3.10) напряжения на входе и выходе
четырехполюсников равны:
ри
параллельном соединении четырехполюсников
(рис. 3.10) напряжения на входе и выходе
четырехполюсников равны: ,
,
 ,
т.е. являются общими для всех
четырехполюсников. Поэтому в качестве
системы, описывающей это соединение,
следует выбирать систему уравнений в
Y–параметрах.
Для схемы (рис. 3.9) справедливо
,
т.е. являются общими для всех
четырехполюсников. Поэтому в качестве
системы, описывающей это соединение,
следует выбирать систему уравнений в
Y–параметрах.
Для схемы (рис. 3.9) справедливо
 .
.
Просуммируем
эти выражения с учетом того, что
 ,
,
 ,
,
 :
:
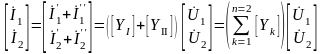 .
.
Если параллельно включено n четырехполюсников, то
 . (3.53)
. (3.53)
Следовательно, при параллельном соединении четырехполюсников матрица Y–параметров есть сумма матриц Y–параметров отдельных четырехполюсников.
3 .11.3. Последовательное соединение
При
последовательном включении
четырехполюсников (рис. 3.11)
 ,
,
 ,
т.е. являются общими для всех
четырехполюсников. Для математического
описания соединения удобно воспользоваться
уравнениями четырехполюсника в
Z–параметрах:
,
т.е. являются общими для всех
четырехполюсников. Для математического
описания соединения удобно воспользоваться
уравнениями четырехполюсника в
Z–параметрах:
 ,
,
 .
.
Просуммируем
эти выражения с учетом того, что
 ,
,
 :
:
 .
.
Если в схеме n четырехполюсников включены по последовательной схеме, то
 . (3.54)
. (3.54)
Таким образом, при последовательном соединении четырехполюсников матрица Z–параметров эквивалентного четырехполюсника равна сумме матриц Z–параметров отдельных четырехполюсников.
Выражения (3.52), (3.53), (3.54) дают возможность перейти от сложных схем соединения четырехполюсников к схемам, состоящим из одного четырехполюсника с соответствующими параметрами эквивалентных матриц.
Билет№4
1.Начальные условия. Законы коммутации.
(смотри Билет№1, вопрос1)
