
- •Билет№1
- •Понятие коммутации цепи. Виды коммутации.
- •2. Четырехполюсники. Понятие, классификация. Обратимость четырехполюсников.
- •Классификация четырехполюсников
- •Режим обратного питания четырехполюсников
- •Билет№2
- •1.Причины возникновения переходного процесса.
- •2.Система уравнений четырехполюсника. Понятие симметрии четырехполюсника. Основные уравнения четырехполюсников
- •3.3. Режим обратного питания четырехполюсников
- •Симметричный четырехполюсник
- •Билет№3
- •1.Составление дифференциальных уравнений цепи. Принципы решения дифференциальных уравнений. Классический метод. Классический метод расчета
- •Классический метод расчёта переходных процессов
- •2.Виды соединений нескольких четырехполюсников. Соединения четырехполюсников
- •3.13.1. Каскадное соединение
- •3.13.2. Параллельное соединение
- •3 .11.3. Последовательное соединение
- •Билет№4
- •1.Начальные условия. Законы коммутации.
- •Общая характеристика переходных процессов
- •2.Четырехполюсники в форме ||z|| параметров.
- •Билет№5
- •1.Классический метод расчета переходных процессов.
- •К лассический метод расчета
- •2.Четырехполюсники в форме ||а|| параметров. Условие его обратимости.
- •Определение а–параметров с помощью режимов короткого замыкания и холостого хода
- •Билет№6
- •1.Подключение цепи r,l к источнику энергии. Время переходного процесса.
- •2.Характеристические параметры четырехполюсника: согласованные сопротивления, мера передачи. Характеристические параметры четырехполюсника
- •Билет№7
- •1.Замыкание цепи r,l с накопленной энергией на себя. Время переходного процесса.
- •2.Четырехполюсник в форме ||а|| параметров в гиперболических функциях. Уравнения четырехполюсника в гиперболических функциях
- •Билет№8
- •1.Подключения цепи r,c к источнику энергии. Время переходного процесса.
- •2.Определение параметров эквивалентного четырехполюсника при последовательном, параллельном и каскадном соединении нескольких четырехполюсников.
- •Билет№9
- •1.Замыкание цепи r,c с накопленной энергией на себя. Время переходного процесса.
- •2.Определение параметров эквивалентного четырехполюсника при смешанном соединении нескольких четырехполюсников. . Эквивалентные схемы замещения четырехполюсника
- •Билет№10
- •1.Особенности расчета переходных процессов в цепях второго порядка классическим методом при действительных корнях характеристического уравнения.
- •4.2.6.1. Разряд емкости на цепь rl
- •Билет№11
- •1.Особенности расчета переходных процессов в цепях второго порядка классическим методом при комплексно-сопряженных корнях характеристического уравнения.
- •2.Вторичные параметры четырехполюсника. Примеры их нахождения. Билет№12
- •1.Подключения цепи r,l,c к источнику энергии. Время переходного процесса.
- •Переходные процессы при подключении последовательной r-l-c-цепи к источнику напряжения
- •2.Электрические фильтры понятие и классификация.
- •Билет№13
- •1.Замыкание цепи r,l,c с накопленной энергией на себя. Время переходного процесса.
- •2.Полоса пропускания и полоса задержки электрических фильтров. Граничные частоты пропускания реактивных фильтров.
Переходные процессы при подключении последовательной r-l-c-цепи к источнику напряжения
Р ассмотрим
два случая:
ассмотрим
два случая:
а)
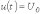 ;
;
б)
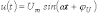 .
.
Согласно изложенной в предыдущей лекции методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать
|
(1) |
Тогда для первого случая принужденная составляющая этого напряжения
|
(2) |
Характеристическое уравнение цепи
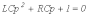 ,
,
решая которое, получаем
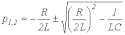 .
.
В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей:
1.
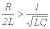 или
или
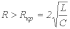 ,
где
,
где
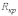 -
критическое
сопротивление
контура, меньше которого свободный
процесс носит колебательный характер.
-
критическое
сопротивление
контура, меньше которого свободный
процесс носит колебательный характер.
В этом случае
|
(3) |
2.
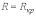 -
предельный случай апериодического
режима.
-
предельный случай апериодического
режима.
В
этом случае
 и
и
|
(4) |
3.
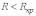 -
периодический (колебательный) характер
переходного процесса.
-
периодический (колебательный) характер
переходного процесса.
В
этом случае
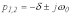 и
и
|
(5) |
где
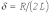 -
коэффициент затухания;
-
коэффициент затухания;
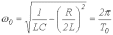 -
угловая
частота собственных колебаний;
-
угловая
частота собственных колебаний;
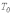 -
период собственных колебаний.
-
период собственных колебаний.
Для апериодического характера переходного процесса после подстановки (2) и (3) в соотношение (1) можно записать
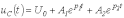 .
.
Для
нахождения постоянных интегрирования,
учитывая, что в общем случае
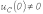 и
в соответствии с первым законом коммутации
и
в соответствии с первым законом коммутации
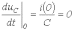 ,
запишем для t=0 два уравнения:
,
запишем для t=0 два уравнения:
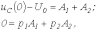
решая которые, получим
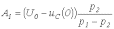 ;
;
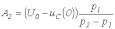 .
.
Таким образом,
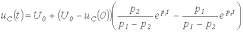 .
.
Тогда ток в цепи

и напряжение на катушке индуктивности
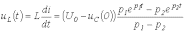
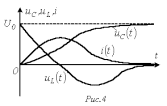 .
.
На
рис. 4 представлены качественные кривые
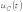 ,
,
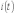 и
и
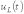 ,
соответствующие апериодическому
переходному процессу при
.
,
соответствующие апериодическому
переходному процессу при
.
Для критического режима на основании (2) и (4) можно записать
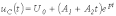 .
.
При
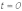
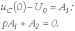
Таким образом
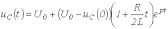
и
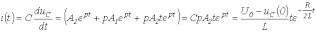 .
.
Для колебательного переходного процесса в соответствии с (2) и (5) имеем
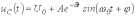 .
.
Для
нахождения постоянных интегрирования
запишем
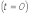
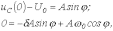
откуда
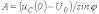 и
и
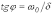 .
.
Тогда

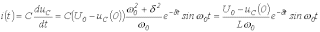 .
.
Н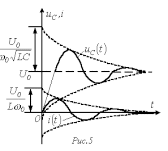 а
рис. 5представлены качественные кривые
а
рис. 5представлены качественные кривые
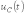 и
,
соответствующие колебательному
переходному процессу при
.
и
,
соответствующие колебательному
переходному процессу при
.
При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым
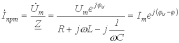
и
 ,
,
где
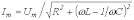 ;
;
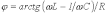 ;
;
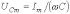 .
.
Таким образом,
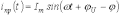 и
и
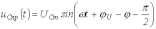 .
.
Здесь также возможны три режима:
1.
|
2.
|
3.
|
|
|
|
Наибольший
интерес представляет третий режим,
связанный с появлением во время
переходного процесса собственных
колебаний с частотой
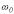 .
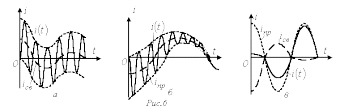
При этом возможны, в зависимости от
соотношения частот собственных колебаний
и напряжения источника, три характерные
варианта: 1 -
.
При этом возможны, в зависимости от
соотношения частот собственных колебаний
и напряжения источника, три характерные
варианта: 1 -
 ;
2 -
;
2 -
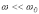 ;
3 -
;
3 -
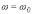 ,
- которые представлены на рис. 6,а…6,в
соответственно.
,
- которые представлены на рис. 6,а…6,в
соответственно.
2.Электрические фильтры понятие и классификация.
Электрическим фильтром называется четырехполюсник, устанавливаемый между источником питания и нагрузкой и служащий для беспрепятственного (с малым затуханием) пропускания токов одних частот и задержки (или пропускания с большим затуханием) токов других частот.
Диапазон частот, пропускаемых фильтром без затухания (с малым затуханием), называется полосой пропускания или полосой прозрачности; диапазон частот, пропускаемых с большим затуханием, называется полосой затухания или полосой задерживания. Качество фильтра считается тем выше, чем ярче выражены его фильтрующие свойства, т.е. чем сильнее возрастает затухание в полосе задерживания.
В качестве пассивных фильтров обычно применяются четырехполюсники на основе катушек индуктивности и конденсаторов. Возможно также применение пассивных RC-фильтров, используемых при больших сопротивлениях нагрузки.
Фильтры применяются как в радиотехнике и технике связи, где имеют место токи достаточно высоких частот, так и в силовой электронике и электротехнике.
Для
упрощения анализа будем считать, что
фильтры составлены из идеальных катушек
индуктивности и конденсаторов, т.е.
элементов соответственно с нулевыми
активными сопротивлением и проводимостью.
Это допущение достаточно корректно при
высоких частотах, когда индуктивные
сопротивления катушек много больше их
активных сопротивлений (
 ),
а емкостные проводимости конденсаторов
много больше их активных проводимостей
(
),
а емкостные проводимости конденсаторов
много больше их активных проводимостей
(
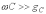 ).
).
Фильтрующие
свойства четырехполюсников обусловлены
возникающими в них резонансными режимами
– резонансами токов и напряжений.
Фильтры обычно собираются по симметричной
Т- или П-образной схеме, т.е. при
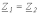 или
или
 (см.
лекцию №14). В этой связи при изучении
фильтров будем использовать введенные
в предыдущей лекции понятия коэффициентов
затухания и фазы.
(см.
лекцию №14). В этой связи при изучении
фильтров будем использовать введенные
в предыдущей лекции понятия коэффициентов
затухания и фазы.
Классификация фильтров в зависимости от диапазона пропускаемых частот приведена в табл. 1.
Таблица 1. Классификация фильтров
Название фильтра |
Диапазон пропускаемых частот |
|||
Низкочастотный фильтр (фильтр нижних частот) |
|
|||
Высокочастотный фильтр (фильтр верхних частот) |
|
|||
Полосовой фильтр (полосно-пропускающий фильтр) |
|
|||
Режекторный фильтр (полосно-задерживающий фильтр) |
где
|
В соответствии с материалом, изложенным в предыдущей лекции, если фильтр имеет нагрузку, сопротивление которой при всех частотах равно характеристическому, то напряжения и соответственно токи на его входе и выходе связаны соотношением
. |
(1) |
В
идеальном случае в полосе пропускания
(прозрачности)
 ,
т.е. в соответствии с (1)
,
т.е. в соответствии с (1)
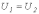 ,
,
 и
и
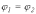 .
Следовательно, справедливо и равенство
.
Следовательно, справедливо и равенство
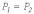 ,
которое указывает на отсутствие потерь
в идеальном фильтре, а значит, идеальный
фильтр должен быть реализован на основе
идеальных катушек индуктивности и
конденсаторов. Вне области пропускания
(в полосе затухания) в идеальном случае
,
которое указывает на отсутствие потерь
в идеальном фильтре, а значит, идеальный
фильтр должен быть реализован на основе
идеальных катушек индуктивности и
конденсаторов. Вне области пропускания
(в полосе затухания) в идеальном случае
 ,
т.е.
,
т.е.
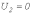 и
и
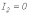 .
.

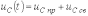 .
. 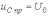 .
. 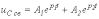 .
. .
.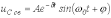 ,
, 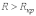 ;
; 
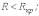
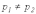
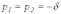

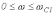
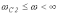
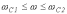
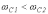
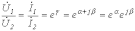 .
.