3. Одномерные нестационарные движения газа

Основные уравнения сохранения, которые справедливы, естественно, и для нестационарного потока, можно преобразовать к виду, при котором в них будут входить комплексы, называемые инвариантами Римана. Инварианты Римана широко используются при расчете нестационарного движения газа и имеют следующий вид:

.

Особенность инвариантов Римана в том, что вдоль характеристического направления в х-t при изоэнтропных плоских движениях газа величина соответствующих инвариантов (при изменении скорости звука с и скорости потока u) остается постоянной.

Необходимо подчеркнуть, что в инварианты Римана входят два параметра – скорость звука или температура и скорость потока, поэтому для определенности необходимо задание еще одного параметра – давления или плотности.

Для упрощения расчетов нестационарного течения газа используются (по аналогии со стационарными течениями) газодинамические функции для изоэнтропных нестационарных течений, связывающие статические параметры потока с параметрами нестационарно заторможенного потока. Поскольку поток газа может быть заторможен нестационарно как волной разрежения, так и волной сжатия, то для каждого параметра состояния используются две газодинамические функции:

для скорости звука

для температуры

для плотности

для давления ,

где с', T', ' и p' – параметры, полученные при торможении потока волной разрежения; с'', T'', '' и p'' – параметры, полученные при торможении потока волной сжатия.

В отличие от простых волн состояние газа на фронте ударной волны изменяется скачком (рис. 3.1) и соотношения параметров имеют следующий вид.

Рис. 3.1

Приращение скорости потока при переходе через ударную волну

,

где М_у – число Маха ударной волны.

Отношение давлений на ударной волне

.

ПРИМЕР

По каналу постоянного поперечного сечения по направлению к открытому концу канала движется волна разрежения с инвариантом Римана I₊₃. Определить инвариант волны, отраженной от открытого конца канала, если инварианты воздуха перед волной равны I₊₀ = I_-0. Давление окружающей среды р₀, коэффициент восстановления полного давления на входе в канал .

Решение

Поскольку инварианты воздуха перед волной равны, то воздух перед волной неподвижен, поэтому можно записать

I₊₀ = I_-0 = I_-3.

Расчетная схема течения показана на рисунке 3.2.

Рис. 3.2

К открытому концу трубопровода подходит волна разрежения, и происходит втекание газа в трубопровод.

Первую и вторую зоны разделяет фронт волны сжатия, отраженной от открытого конца канала; вторую и третью зоны – контактная поверхность.

Для решения задачи необходимо задать два граничных условия. Граничные условия получают из предположения об установившемся адиабатическом втекании газа из окружающей среды в трубопровод

.

Определим число Маха в третьей зоне по инвариантам Римана. Скорость потока

.

Скорость звука в потоке

.

Число Маха

M₃ = u₃/с₃.

Давление в третьей зоне

p₃ = p₀(M₃).

Запишем тождество

.

Выразим параметры уравнения через газодинамические функции и известные параметры.

Из второго граничного условия получим

.

Отношение давлений на фронте волны

.

Давления слева и справа от контактной поверхности равны

.

Подставим в тождество эти параметры. Тогда оно будет иметь вид

. (3.1)

В уравнении (3.1) два неизвестных – М₂ и М₁. Из равенства скоростей на контактной поверхности можем получить второе уравнение

с₁М₁ = с₂М₂.

Выразим скорости звука через известные параметры и газодинамические функции. Из первого граничного условия получим

.

Отношение скоростей звука на фронте волны

.

Тогда

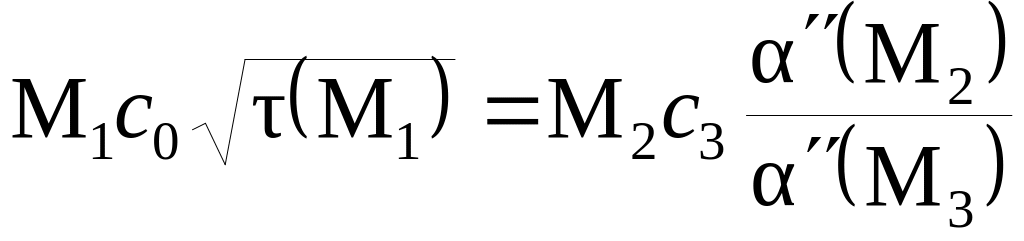. (3.2)

Решая систему уравнений (3.1) и (3.2), находим M₂ и M₁.

Инвариант отраженной волны находится по уравнению

.

ЗАДАЧИ

Задача 3.1. По каналу движется волна сжатия, перед которой воздух неподвижный. Избыточное давление в волне равно 0,15 МПа, давление и температура неподвижного воздуха соответственно равны 0,1 МПа и 290 К. Определить инварианты Римана в волне и в неподвижной среде.

Задача 3.2. Поршень, находящийся в канале постоянного поперечного сечения начал двигаться с ускорением 1000 м/с² и через 0,1 с остановился. Определить максимальные давление и температуру в волне, возбужденной в канале справа от поршня и ее длину. Начальные параметры воздуха в канале: p₀ = 0,1 МПа, T₀ = 270 K.

Задача 3.3. По каналу движется волна сжатия, давление в которой равно 0,2 МПа. Перед волной движется поршень со скоростью 100 м/с. Параметры газа между волной и поршнем р₀ = 0,1 МПа, Т₀ = 300 К. В начальный момент времени расстояние между поршнем и волной равно 1 м. Определить время, за которое волна догонит поршень, давление за поршнем и инвариант отраженной от поршня волны после взаимодействия волны и поршня.

Задача 3.4. В канале постоянного поперечного сечения на расстоянии 0,5 м друг от друга расположены два поршня (рис. 3.3). В некоторый момент времени они мгновенно начинают двигаться со скоростью u_п = 50 м/с в одну сторону. Построить график изменения давления по длине трубопровода в момент времени 0,0005 с от начала движения. Начальное давление равно 0,1 МПа, начальная температура равна 273 К. Трение и теплообмен отсутствуют. Воздух до начала движения был неподвижным.

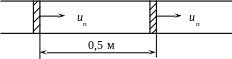
Рис. 3.3

Задача 3.5. По каналу постоянного поперечного сечения по направлению к открытому концу канала движется простая волна сжатия. Определить при каком давлении скорость истечения воздуха на открытом конце будет равна местной скорости звука, если параметры воздуха перед волной и в окружающей среде равны соответственно 0,1 МПа и 273 К.

Задача 3.6. По каналу постоянного поперечного сечения по направлению к открытому концу канала движется волна разрежения. Определить при каком давлении в волне скорость втекания воздуха в канал будет равна местной скорости звука, если давление и температура воздуха перед волной и в окружающей среде равны соответственно 0,1 МПа и 273 К. Потерями на входе в канал пренебречь.

Задача 3.7. По каналу постоянного поперечного сечения навстречу друг другу движутся поршень со скоростью u_п = 70 м/с и волна сжатия, инвариант Римана которой равен 2000 м/с (рис. 3.4). Определить инварианты волны, отраженной от поршня.

Рис. 3.4

Задача 3.8. По каналу постоянного поперечного сечения по направлению к открытому концу канала движется волна с инвариантом, равным 1600 м/с. Определить инвариант отраженной от открытого конца волны, если инварианты в канале перед волной и в окружающей среде равны 1700 м/с. Потери на входе в канал не учитывать.

Задача 3.9. По каналу постоянного поперечного сечения по направлению к открытому концу канала движется волна разрежения, избыточное давление в которой равно -0,07 МПа. Определить давление в волне, отраженной от открытого конца канала, если давление и температура воздуха в канале перед волной и в окружающей среде соответственно равны 0,1 МПа и 273 К. Коэффициент восстановления полного давления на входе в канал  = 0,9.

Задача 3.10. По каналу постоянного поперечного сечения по направлению к открытому концу канала движется волна сжатия, избыточное давление в которой равно 0,05 МПа. Определить давление в волне, отраженной от открытого конца канала, если давление и температура воздуха в канале перед волной и в окружающей среде соответственно равны 0,1 МПа и 273 К.

Задача 3.11. По каналу постоянного поперечного сечения навстречу друг другу движутся две волны сжатия с максимальными давлениями 0,15 МПа и 0,2 МПа (рис. 3.5). Определить максимальное давление в канале после наложения волн друг на друга. Начальные параметры в канале: р₀ = 0,1 МПа и Т₀ = 273 К.

Рис. 3.5

Задача 3.12. По каналу постоянного поперечного сечения навстречу друг другу движутся две волны сжатия с инвариантами I₊₁ = 1800 м/с и I_-2 = 2000 м/с. Построить в координатах "длина-время" траектории движения инвариантов I₊₁ и I_-2 до и после их встречи. Температура неподвижного воздуха в канале перед волной равна 273 К.

Задача 3.13. Считая течение изоэнтропным, найти давление перед диафрагмой, установленной на конце канала, если избыточное давление в волне, подходящей к диафрагме равно р_в = 0,05 МПа, а параметры неподвижного воздуха в канале р₀ = 0,1 МПа и Т₀ = 273 К (рис. 3.6). Отношение площади отверстия к площади канала составляет 0,4.

Рис. 3.6

Задача 3.14. Определить давление в волне, прошедшей через диафрагму, которая установлена в канале постоянного поперечного сечения (рис. 3.7). Избыточное давление в исходной волне р_в = 0,05 МПа, давление и температура невозмущенного воздуха в канале р₀ = 0,1 МПа и Т₀ = 273 К. Отношение площади отверстия к площади канала составляет 0,6. Коэффициент восстановления полного давления на диафрагме  = 0,8.

Рис. 3.7

Задача 3.15. По каналу постоянного поперечного сечения по направлению к открытому концу канала движется волна сжатия, избыточное давление в которой равно 0,4 МПа. Определить давление на срезе канала, если начальные параметры воздуха р₀ = 0,1 МПа и Т₀ = 273 К.

Задача 3.16. Определить давление в волне, прошедшей в узкую часть канала, если избыточное давление в волне, двигавшейся по широкому каналу р_в = 0,08 МПа (рис. 3.8). Отношение площадей каналов равно 2, коэффициент восстановления полного давления на скачке сечения  = 0,9. Начальные параметры в канале: р₀ = 0,1 МПа и Т₀ = 273 К.

Рис. 3.8

Задача 3.17. Определить давление в волне, отраженной от скачка сечения (внезапного расширения канала) и инвариант отраженной волны, если избыточное давление в волне, двигавшейся к скачку сечения равно 0,05 МПа. Отношение площадей каналов равно 3, коэффициент восстановления полного давления на скачке сечения  = 0,8. Начальные параметры в канале: р₀ = 0,1 МПа и Т₀ = 273 К.