
- •1.Понятие производной функции.Непрерывность и дифференцируемость функций.
- •6.Произ.Высших порядков.
- •7 .Производные неявной ф-ии.
- •10. Диф.Высших порядков.
- •11. Основные теоремы дифференциального исчисления (теоремы о среднем).
- •12. Применение производной к вычислению пределов. Теорема Лопиталя – Бернулли.
- •Отношение бесконечно больших
- •13. Возрастание и убывание функций. Необходимое и достаточное условия.
- •14. Экстремумы функции. Необходимое и достаточные условия.
- •Алгоритм.
- •Третий достаточный признак экстремума функции.
- •15. Наибольшее и наименьшее значения функции
- •16. Направление выпуклости и точки перегиба графика функции. Необходимые и достаточные условия.
- •Определения и понятия.
- •17. Асимптоты графика функции, их виды и условия существования.
- •18. Общая схема исследования функций и построения их графиков.
- •19. Функции 2-х и 3-х переменных: способы задания, область определения и графики.
- •20. Частные производные 1-го порядка функции 2-х переменных. Их геометрический смысл.
- •Определение 1.7 Если существует конечный предел отношения частного приращения по X функции f(X,y,z) в точке m0(x0,y0,z0) к вызвавшему его
- •24. Полный дифференциал фнп. Инвариантность его формы.
- •Теорема об инвариантности дифференциала
- •25. Приложения полного дифференциала к приближенным вычислениям.
- •28. Неявные фнп и их дифференцирование.
- •29. Экстремум фнп. Необходимое и достаточные условия экстремума.
- •50. Несобственные интегралы от бесконечных функций (|| рода).
- •53. Приближенные методы вычисления определенных интегралов.
53. Приближенные методы вычисления определенных интегралов.
Основой
способов приближенного интегрирования
является определение интеграла
как предела интегральных сумм. Известно,
что понятие определенного интеграла
вводится следующим образом. Пусть на
отрезке [a,b] определена
функция f(x).
Интегральной суммой называется выражение:
![]()
Для приближенного вычисления интегралов чаще всего подынтегральную функцию заменяют «близкой» к ней вспомогательной функцией, интеграл от которой можно вычислить. За приближенное значение интеграла принимают значение интеграла от вспомогательной функции (например, площадь криволинейной трапеции заменяют площадью прямоугольника или прямолинейной трапеции, то есть вспомогательной является линейная функция).
1.
Формула трапеций.
Пусть требуется вычислить интеграл

, где f(x) - непрерывная функция. Для простоты рассуждений ограничимся случаем,
когда f(x)³0. Разобьем отрезок [a, b] на n отрезков точками a=x0
<x1<x2<...<xk-1<xk
<...<xn=b и с помощью прямых х=хk построим n
прямолинейных трапеций (эти трапеции заштрихованы на рис. 1). Сумма площадей
трапеций приближенно равна площади криволинейной трапеции, т.е.
Где f(xk-1) и f(xk) - соответственно основания трапеций;
xk - xk-1 = (b-a)/n - их высоты.
Таким
образом, получена приближенная формула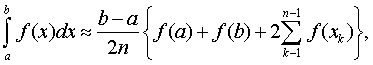
|
которая и называется формулой трапеций. Эта формула тем точнее, чем больше n.
Ф-ла Симпсона
Ф-ла
прямоугольника сумма S является
интегральной для функции f(x)
на отрезке [a,b],
поэтому приближенно равна интегралу:
![]() Таким
образом, площадь криволинейной трапеции
аппроксимируется (приближается) площадью
ступенчатой фигуры, состоящей из
прямоугольников. Формула (1) называется
формулой «правых» прямоугольников.Аналогично,
рассматривая в качестве высоты каждого
прямоугольника левую ординату, можно
получить формулу «левых» прямоугольников:
Таким
образом, площадь криволинейной трапеции
аппроксимируется (приближается) площадью
ступенчатой фигуры, состоящей из
прямоугольников. Формула (1) называется
формулой «правых» прямоугольников.Аналогично,
рассматривая в качестве высоты каждого
прямоугольника левую ординату, можно
получить формулу «левых» прямоугольников:
![]()
Известно,
что через три заданные точки, не лежащие
на одной прямой, можно провести параболу
единственным образом, поэтому отрезок
интегрирования [a,b]
надо разбить на n частей
таким образом, чтобы полученные точки
деления позволяли построить
параболы. Очевидно,
что число точек деления должно быть
четным: n =
2m.
Границами промежутков будут точки ![]() ,
а длина каждого промежутка равна
,
а длина каждого промежутка равна 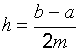 .
Пусть
.
Пусть ![]() .
Рассмотрим первые два промежутка
деления. Функцию f(x)
на отрезке
.
Рассмотрим первые два промежутка
деления. Функцию f(x)
на отрезке![]() заменим
параболой, проходящей через точки
заменим
параболой, проходящей через точки ![]() .
Будем искать уравнение параболы в виде
многочлена второй степени.
.
Будем искать уравнение параболы в виде
многочлена второй степени.
![]() . (5)
. (5)
Неизвестные
коэффициенты А, В, С найдем из условий ![]()
![]() .
Подставим в формулу (5) значение
.
Подставим в формулу (5) значение![]() ,
получим
,
получим ![]() .
Поскольку
.
Поскольку ![]() ,
то
,
то ![]() ,
откуда
,
откуда  .
Аналогично, при
.
Аналогично, при ![]() ,
получим
,
получим ![]() и
и  ,
а при
,
а при ![]() найдем
коэффициент
найдем
коэффициент  .
Заменив площадь криволинейной трапеции,
ограниченной кривой y = f(x),
на площадь криволинейной трапеции,
ограниченной параболой, получим
приближенную формулу:
.
Заменив площадь криволинейной трапеции,
ограниченной кривой y = f(x),
на площадь криволинейной трапеции,
ограниченной параболой, получим
приближенную формулу:

Введем
замену переменной ![]() ,тогда
данный интеграл примет вид:
,тогда
данный интеграл примет вид:
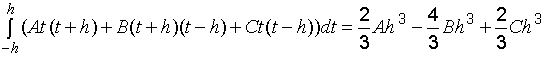 .
.
Воспользуемся найденными значениями для А, В, С и запишем:
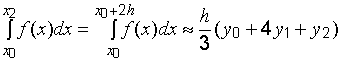 . (6)
. (6)
Теперь для всего промежутка [a,b] можно указать формулу приближенного вычисления:
![]()
или
![]() .
(7)
.
(7)
Формула (7) называется формулой Симпсона.
.
