
- •1.Понятие производной функции.Непрерывность и дифференцируемость функций.
- •6.Произ.Высших порядков.
- •7 .Производные неявной ф-ии.
- •10. Диф.Высших порядков.
- •11. Основные теоремы дифференциального исчисления (теоремы о среднем).
- •12. Применение производной к вычислению пределов. Теорема Лопиталя – Бернулли.
- •Отношение бесконечно больших
- •13. Возрастание и убывание функций. Необходимое и достаточное условия.
- •14. Экстремумы функции. Необходимое и достаточные условия.
- •Алгоритм.
- •Третий достаточный признак экстремума функции.
- •15. Наибольшее и наименьшее значения функции
- •16. Направление выпуклости и точки перегиба графика функции. Необходимые и достаточные условия.
- •Определения и понятия.
- •17. Асимптоты графика функции, их виды и условия существования.
- •18. Общая схема исследования функций и построения их графиков.
- •19. Функции 2-х и 3-х переменных: способы задания, область определения и графики.
- •20. Частные производные 1-го порядка функции 2-х переменных. Их геометрический смысл.
- •Определение 1.7 Если существует конечный предел отношения частного приращения по X функции f(X,y,z) в точке m0(x0,y0,z0) к вызвавшему его
- •24. Полный дифференциал фнп. Инвариантность его формы.
- •Теорема об инвариантности дифференциала
- •25. Приложения полного дифференциала к приближенным вычислениям.
- •28. Неявные фнп и их дифференцирование.
- •29. Экстремум фнп. Необходимое и достаточные условия экстремума.
- •50. Несобственные интегралы от бесконечных функций (|| рода).
- •53. Приближенные методы вычисления определенных интегралов.
1.Понятие производной функции.Непрерывность и дифференцируемость функций.
Пусть f(x)
нек.ф-ия опред на интервале (а;в) и х(фикс
точка) принадлежит (а;в) возьмем произв
т.х из инт ав разность (х- )-приращ
арг f(x)
и обознач
)-приращ
арг f(x)
и обознач
 x=х-
.
Приращ ф-ии f(x)
в т.
назыв разность между знач ф-ии в т. х и
.
f(x)=f(x)-f(
)=f(
+
x)-f(
)
т.к. х0-фикс то f(x)
от
x
–явл приращ произв f(x)
в т.
-предел
отнош прир ф-ии f(x)
x
к соотв прир арг дельтаХ когда
x(
)
стрем к 0: f
`(
)
x=х-
.
Приращ ф-ии f(x)
в т.
назыв разность между знач ф-ии в т. х и
.
f(x)=f(x)-f(
)=f(
+
x)-f(
)
т.к. х0-фикс то f(x)
от
x
–явл приращ произв f(x)
в т.
-предел
отнош прир ф-ии f(x)
x
к соотв прир арг дельтаХ когда
x(
)
стрем к 0: f
`(
)
 (1!)
Если предел(1!) сущ,то гов.что ф-ия f(x)
име. Произв в т.
или ф-ия диффиринцируема в т.
Непрерывность
дифференцируемой функции
(1!)
Если предел(1!) сущ,то гов.что ф-ия f(x)
име. Произв в т.
или ф-ия диффиринцируема в т.
Непрерывность
дифференцируемой функции
Теорема 1. Пусть
функция y =
f(x)
дифференцируема на интервале (a,
b). Тогда
функция f
непрерывна
на (a,
b).Возьмем
произвольное фиксированное число x
 (a,b).По
условию теоремы
(a,b).По
условию теоремы
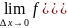 Следовательно,
в малой окрестности числа x0
можно определить функцию α
= α(Δx),
стремящуюся к нулю при
Следовательно,
в малой окрестности числа x0
можно определить функцию α
= α(Δx),
стремящуюся к нулю при
 такую, что
такую, что
 Но тогда и, следовательно, функция f
непрерывна при x
= x0.
Так как число x0
– произвольное, то функция f
непрерывна на всем интервале (a,
b). f(
Но тогда и, следовательно, функция f
непрерывна при x
= x0.
Так как число x0
– произвольное, то функция f
непрерывна на всем интервале (a,
b). f(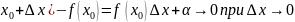 .Теорема
доказана.Из
доказанной теоремы непосредственно
вытекает, что в точках разрыва функция
не может быть дифференцируемой.Однако
из непрерывности функции на интервале
(a, b)
не следует дифферецируемость функции
в каждой точке интервала (a,
b). Например,
функция y=
.Теорема
доказана.Из
доказанной теоремы непосредственно
вытекает, что в точках разрыва функция
не может быть дифференцируемой.Однако
из непрерывности функции на интервале
(a, b)
не следует дифферецируемость функции
в каждой точке интервала (a,
b). Например,
функция y=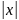 непрерывна на всей числовой прямой, но
эта функция недифференцируема при x
= 0. В самом
деле, предел (1) не зависит от знака
приращения аргумента Δx.
Для функции же y=
имеем,
если x = 0
придать приращение Δx
> 0, то Δy
= Δx, а если
Δx < 0, то
Δy = − Δx.
Таким образом,
непрерывна на всей числовой прямой, но
эта функция недифференцируема при x
= 0. В самом
деле, предел (1) не зависит от знака
приращения аргумента Δx.
Для функции же y=
имеем,
если x = 0
придать приращение Δx
> 0, то Δy
= Δx, а если
Δx < 0, то
Δy = − Δx.
Таким образом,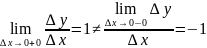 .Следовательно,
функция y=
недифференцируема при x
= 0.
Дифференцируемость ф-ии: Если f
диф в нек. т.
,
то она не прерывна в этой точке. Док-во.
Пусть арг. х в т.
получ.прир.
.Следовательно,
функция y=
недифференцируема при x
= 0.
Дифференцируемость ф-ии: Если f
диф в нек. т.
,
то она не прерывна в этой точке. Док-во.
Пусть арг. х в т.
получ.прир.
 если соотв нек прир ф-ии
если соотв нек прир ф-ии
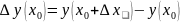 рассмотрим очер.тождество
рассмотрим очер.тождество
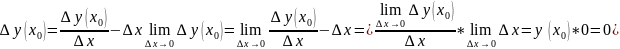 ф-ия у=f(x)
– непрер в т.0 обрат.т.НЕ ВЕРНА! Сущ непрер
ф-ии кот в нек.т.не явл. диф.
ф-ия у=f(x)
– непрер в т.0 обрат.т.НЕ ВЕРНА! Сущ непрер
ф-ии кот в нек.т.не явл. диф.
2.Непосредственное нахождение производной.
Произв.люб ф-ии в тех случаях,когда ее сумму можно найти исходя из (1!)
3. Основные правила и формулы дифференцирования.
В ыч.произпо
опред.к дост.сл.выкладкам поэтому в
анализе был предложен ед.мет.позв.нах.произв.для
очень шир.класса ф-ии(в том числе для
люб эл-та ф-ии) при помощи осн. Ф-л и
прав.диф.
ыч.произпо
опред.к дост.сл.выкладкам поэтому в
анализе был предложен ед.мет.позв.нах.произв.для
очень шир.класса ф-ии(в том числе для
люб эл-та ф-ии) при помощи осн. Ф-л и
прав.диф.
4.Лографмическое дифф.
Прием логарифм
дифф исп когда ф-ия имеет вид удобн.для
лог и свод к след схеме 1)ф-ию y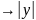 2)log
2)log
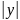 3)нах
произв.(log|y|)`
помня,что есть ф-ия от х 4) из получ рав-ва
у`
3)нах
произв.(log|y|)`
помня,что есть ф-ия от х 4) из получ рав-ва
у`
5.Геом.Смысл произв.Касательная и нормаль к плоской кривой.
Г еометрический
смысл производной.
Производная в точке x 0
равна угловому коэффициенту касательной
к графику функции y
= f(x)
в этой точке.
еометрический
смысл производной.
Производная в точке x 0
равна угловому коэффициенту касательной
к графику функции y
= f(x)
в этой точке.
Рассмотрим график функции y = f ( x ):

Из
рис.1 видно, что для любых двух точек A
и B
графика функции:
![]() xf(x0+
x)−f(x0)=tg
xf(x0+
x)−f(x0)=tg![]() ,
где
,
где
![]() -
угол наклона секущей AB.
Таким образом, разностное отношение
равно угловому коэффициенту секущей.
Если зафиксировать точку A
и двигать по направлению к ней точку B,
то
-
угол наклона секущей AB.
Таким образом, разностное отношение
равно угловому коэффициенту секущей.
Если зафиксировать точку A
и двигать по направлению к ней точку B,
то
![]() x
неограниченно уменьшается и приближается
к 0, а секущая АВ
приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A.
Отсюда
следует:производная функции в точке
есть угловой коэффициент касательной
к графику этой функции в этой точке.В
этом и состоит геометрический смысл
производной.
x
неограниченно уменьшается и приближается
к 0, а секущая АВ
приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A.
Отсюда
следует:производная функции в точке
есть угловой коэффициент касательной
к графику этой функции в этой точке.В
этом и состоит геометрический смысл
производной.
