1. Закон Кулона. Принцип суперпозиции. Закон сохранения заряда.

Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами.

Был открыт Шарлем Кулоном в 1785 г.

Точечный заряд — это заряд, размерами носителя которого по сравнению с расстоянием, на котором рассматривается электростатическое взаимодействие, можно пренебречь.

Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними

где  — сила, с которой заряд 1 действует на заряд 2;  — величина зарядов;  — радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами — );  — коэффициент пропорциональности. Таким образом, закон указывает, что одноимённые заряды отталкиваются (а разноимённые — притягиваются).

где  ≈ 8,854187817·10⁻¹² Ф/м — электрическая постоянная.

При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:

результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.

Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.

Закон сохранения электрического заряда гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.

Электри́ческий заря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. Впервые электрический заряд был введён в законе Кулона в 1785 году.

Система называется электрически изолированной если через ограничивающую её поверхность не могут проникнуть заряженные частицы

Кл^[1] — заряд электрона.

2. Теорема Гаусса для электростатического поля в вакууме. Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

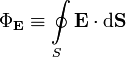 — поток вектора напряжённости электрического поля через замкнутую поверхность

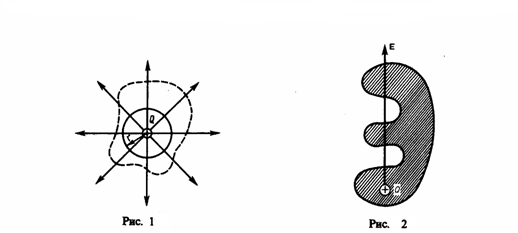
Этот результат справедлив для замкнутой поверхности произвольной формы. Действительно, если заключить сферу (рис. 1) в произвольную замкнутую поверхность, то каждая линия напряженности, которая пронизывает сферу, пройдет и сквозь эту поверхность. В случае, если замкнутая поверхность любой формы охватывает заряд (рис. 2), то при пересечении любой линии напряженности с поверхностью она то входит в нее, то выходит из нее. При вычислении потока нечетное число пересечений в конечном счете сводится к одному пересечению, так как поток полагается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий, которые входят в поверхность.

3. Расчет полей с центральной, осевой и плоской симметрией.

Операции симметрии приводят к тому что объект на который действует такая операция совпадает сам с собой 1)центральная симметрия(сферическая) 2)осевая(цилиндр) 3)плоская(бесконечная плоскость)

Расчет симметричных полей.Теорема Гаусса, в случае симметричных полей (когда Е и cos( ) можно вынести за скобку), применяется для нахождения закона (формулы) напряженности электрического поля неподвижных зарядов (электростатического поля) как функции суммарного заряда (назависимо от его способа распределения внутри поверхности), координат и свойств физической среды

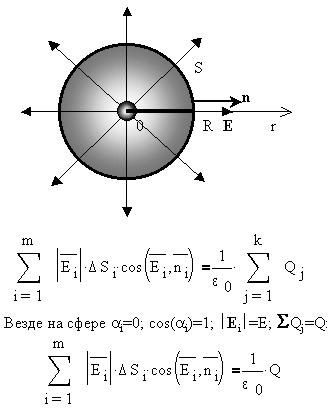
Поле точечного заряда. Как мы уже видели, поле такого заряда имеет сферическую (центральную) симметрию, и если выбрать такого же типа симметрии поверхность,- сферу с центром, совпадающим с зарядом, - то везде на сфере, в силу равноудаленности её поверхности от заряда, модуль напряженности поля будет постоянным, а угол между вектором напряженности и вектором нормали к поверхности равен 0, так как оба направлены по радиусу сферы:

Поле равномерно заряженной бесконечной плоскости.

Введем понятие поверхностной плотности заряда >0, численно равной заряду единицы площади:

В силу однородности и изотропности пространства силовые линии поля равномерно заряженной бесконечной плоскости должны быть перпендикулярными к ней и иметь равномерную густоту, что соответствует определению однородности поля Е=const. В качестве "удобной" замкнутой поверхности выберем прямой цилиндр, боковая поверхность которого параллельна силовым линиям (везде на ней 0 и, следовательно, поток сквозь нее равен 0), а торцевые поверхности площадью S - параллельны заряженной плоскости (так что везде на них 1):

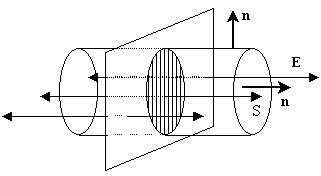
Поток однородного поля Е сквозь обе перпендикулярные ему торцевые поверхности S равен просто Е2S, а заряд, сосредоточенный на участке площадью S заряженной поверхности, равен S:

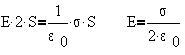
Поле двух бесконечных параллельных разноименно заряженных плоскостей.

Однородные поля таких плоскостей будут отличаться лишь направленностью силовых линий (модули поверхностных плотностей заряда одинаковы):

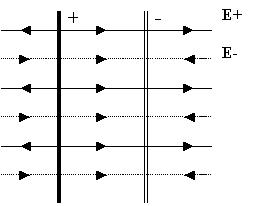
Из рисунка видно, что вне области между плоскостями их поля взаимно "погашаются", и внутри - суммируются: