34.Баланс сил в циклоне и антициклоне. Выражения для скорости ветра.

(1)

С хема градиентного ветра при круговых изобарах имеет большое практическое значение, т.к. она дает простую модель движений воздуха в основных барических образованиях, встречающихся в атмосфере – циклонах и антициклонах. Циклон-барическая обл, ограниченная семейством замкнутых изобар, с минимумом давления в центре; антициклон – барическая обл, но с мах давлением в центре. Свойства градиентного ветра: 1) величина скорости вдоль каждой траектории – круговой изобары – остается постоянной; 2) вертикальные скорости отсутствуют; 3) основным уравнением для градиентного ветра при круговых изобарах явл уравнение:

Все величины, входящие в уравнение, постоянны вдоль каждой траектории – круговой изобары.

Т.к. координата s, вдоль которой отсчитывается скорость V, направлена по движению, то величина V существенно положительна. Радиус кривизны R_T положителен, если траектории вдоль движения поворачивают влево, и отрицателен в противоположном случае. Величина w_z=w*sin (фи) положительна в северном полушарии и отрицательна в южном. Величина положительна, если давление растет влево от движения, и отрицательна, если убывает.

С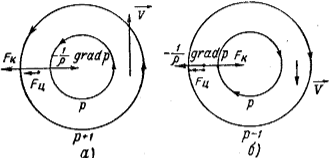 еверное полушарие: траектории вдоль движения поворачивают влево (R_T >0) Т.к. оба члена левой части уравнения (1) положительны, то должно быть т.е. влево от движения давление убывает, а значит, соблюден барический закон ветра. В центре – минимум давления. Это – схема циклона в северном полушарии. (рис. а). Траектории вдоль движения поворачивают вправо ((R_T <0). Тогда знак левой ( а значит, и правой) части уравнения (1) зависит от соотношения абсолютных величин членов, т.е от отношения 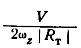. При условии 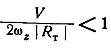, когда малые скорости при больших радиусах кривизны изобар, левая часть уравнения (1) положительна, следовательно, т.е. влево от движения давление убывает – соблюден барический закон ветра. В центре – мах давления. Это схема антициклона ( рис. б).

В каждой точке циклона барический гра­диент направлен по радиусу к центру.

Как следует из рис. б, отклоняющая сила F_K в антициклоне уравновешивает барический градиент grad p и центробежную силу F_ц : F_{K =} grad p ₊ F_ц. В центре стационарного антициклона (r= 0) ветер обращается в нуль: С удалением от центра скорость градиентного ветра растет (если grad p остается неизменным).

В отличие от циклона, где барический градиент, а вместе с ним и скорость градиентного ветра могут принимать любые, в том числе и очень большие значения, барический градиент и скорость градиентного ветра в антициклоне ограничены. В самом деле в антициклоне давление убывает с уда­лением от центра.

35.Уравнение движения в натуральных координатах. Прямое и обратное преобразование с декартовыми координатами. Наряду с обычными прямолинейными координатами введем криволинейные координаты n и s. Координатные линии направим вдоль скорости ветра в каждый рассматриваемый момент времени, тогда семейство координатных линий s (n=const) будет семейством линий тока . Координатные линии n (s=const) в рассматриваемый момент направим так, чтобы в каждой точке касательная к s=const была перпендикулярна касательной к n=const в той же точке; иначе говоря семейство координатных линий n должно быть ортогонально семейству координатных линий s. Это натуральная система координат (СК).

Д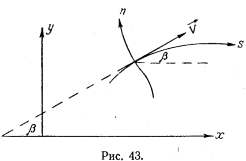 ля того, чтобы представить уравнения движения в натуральных координатах, выведем необходимые для такого преобразования формулы. Прежде всего очевидно (рис.43) что:

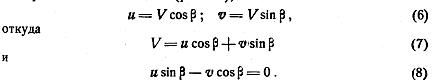
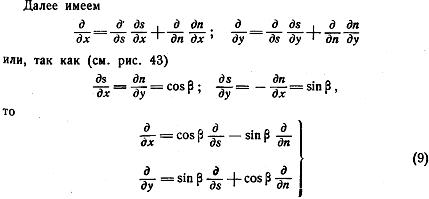
Преобразовав, получим:

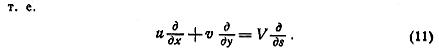
Найдем далее выражение для двух важных характеристик движения – горизонтальной дивергенции скорости и вертикальной составляющей вихря скорости С помощью формул (6) и (9) получаем: (12) и (13).

Горизонтальная дивергенция скорости определяется двумя факторами – изменением модуля скорости вдоль линий тока и сходимостью или расходимостью линий тока. Величину называют иногда дивергенцией модуля скорости. Она дает положительное слагаемое, если скорость растет вдоль потока, и отрицательное – если убывает. Вертикальная составляющая вихря скорости определяется двумя факторами – изменением модуля скорости в направлении, поперечном движению, и кривизной линий тока. Величину наз вихрем модуля скорости, она дает положительное слагаемое, если скорость растет вправо от направления движения, и отрицательное, если скорость растет влево от направления движения.

Выведенные выражения для горизонтальной скорости и вертикальной составляющей вихря скорости в натуральных координатах ценны прежде всего тем, что позволяют отчетливо выявить кинематическую природу этих величин.

П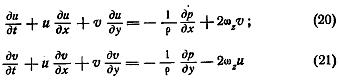 ерейдем к уравнению движения; пренебрегая членами, содержащими вертикальные скорости, запишем эти уравнения в виде:

и приведем их к натуральным координатам.

Умножив (20) на сosβ и (21) на sinβ и сделав необходимые преобразования, получим: Это первое из уравнений движения в натуральной СК, а именно уравнение движения в проекции на линию тока. Введя еще полную производную dV/dt (изменение модуля скорости при движении), которая равна можно записать уравнение движения в виде:

Для получения второго уравнения движения в натуральных координатах умножим (21) на сosβ и (20) на sinβ и из первого результата вычтем второй. Получим: Это 2-е уравнение движения в натуральной СК, а именно уравнение движения в проекции на направление, ортогональное линиям тока. Вводя с помощью формул радиус кривизны траектории R_T, можно переписать уравнение движения в виде: .