21. Предел функции х→∞и при х→х0. Односторонние пределы. Свойства пределов.

Определение. Если по некоторому закону каждому натуральному числу поставлено в соответствие вполне определенное число , то говорят, что задана числовая последовательность :

.

Другими словами, числовая последовательность - это функция натурального аргумента: .

Числа называются членами последовательности, а число - общим или -м членом данной последовательности.

Примеры числовых последовательностей:

1) (монотонная, неограниченная),

2) (не монотонная, ограниченная)

3)

Рассмотрим числовую последовательность , изобразив ее точками на числовой оси (рис.4.1):

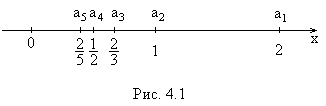
Видно, что члены последовательности с ростом как угодно близко приближаются к 0. При этом абсолютная величина разности становится все меньше и меньше.

Определение. Число называется пределом числовой последовательности , если для любого, даже сколь угодно малого положительного числа , найдется такой (зависящий от ), что для всех членов последовательности с номерами верно неравенство:

.

Обозначают: . Или при .

Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.

Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

22. Числовые последовательности и их пределы. Свойства пределов.

23. Бесконечно малые величины. Сравнение бесконечно малых. Бесконечно малые величины

Определение. Функция называется бесконечно малой величиной при или при , если ее предел равен нулю:

.

Связь бесконечно малых величин с пределами функций

Теорема 1. Если функция имеет при ( ) предел, равный , то ее можно представить в виде суммы этого числа и бесконечно малой при ( ), т.е.

.

Теорема 2. Если функцию можно представить как сумму числа и бесконечно малой при ( ), то число есть предел этой функции при ( ), т.е.

.