Понятие функции одной переменной

Постоянной величиной называется величина, сохраняющая одно и то же значение. Например, отношение длины окружности к ее диаметру есть постоянная величина, равная числу .

Если величина сохраняет постоянное значение лишь в условиях данного процесса, она называется параметром.

Переменной называется величина, которая может принимать различные числовые значения. Например, при равномерном движении: , где - путь, - время, - параметр.

Определение. Если каждому элементу множества ставится в соответствие вполне определенный элемент множества , то тогда говорят, что на множестве задана функция .

При этом называется независимой переменной (или аргументом), - зависимой переменной, а буква обозначает закон соответствия.

Множество называется областью определения (или существования) функции, а множество - областью значений функции.

Если множество специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной , т.е. множество таких значений , при которых функция вообще имеет смысл.

Способы задания функций:

а) Аналитический способ, если функция задана формулой вида . Этот способ наиболее часто встречается на практике.

Например, функция задана аналитически. Не следует, однако, смешивать функцию с ее аналитическим выражением. Так, например, одна функция имеет два аналитических выражения: (при ) и (при ).

б) Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента и соответствующие значения функции , например, таблица логарифмов, гармонические функции и т.д.

, , .

в) Графический способ состоит в изображении графика функции - множества точек плоскости, абсциссы которых есть значения аргумента , а ординаты – соответствующие им значения функции .

г) Словесный способ, если функция описывается правилом ее составления, например, функция Дирихле: , если - иррационально.

18. Основные элементарные функции. Степенная, показательная, логарифмическая, тригонометрическая и обратная тригонометрическая функции. Область определения. Область значения. Графики. Элементарные функции.

1. постоянная  ;

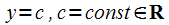2. степенная 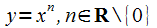, 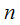задано;

3. показательная ;

4. логарифмическая ;

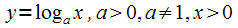5. тригонометрические  ;

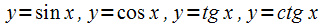6. обратные тригонометрические ;

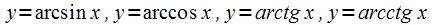Понятие функции одной переменной

Постоянной величиной называется величина, сохраняющая одно и то же значение. Например, отношение длины окружности к ее диаметру есть постоянная величина, равная числу .

Если величина сохраняет постоянное значение лишь в условиях данного процесса, она называется параметром.

Переменной называется величина, которая может принимать различные числовые значения. Например, при равномерном движении: , где - путь, - время, - параметр.

Определение. Если каждому элементу множества ставится в соответствие вполне определенный элемент множества , то тогда говорят, что на множестве задана функция .

При этом называется независимой переменной (или аргументом), - зависимой переменной, а буква обозначает закон соответствия.

Множество называется областью определения (или существования) функции, а множество - областью значений функции.

Если множество специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной , т.е. множество таких значений , при которых функция вообще имеет смысл.