
- •Свойства определителей
- •Алгоритм вычисления обратной матрицы.
- •Элементарные преобразования матрицы:
- •Метод обратной матрицы.
- •Условие совместимости линейных уравнений. Теоремы о числе решений (без доказательств).
- •14. Методы Гаусса решения слау.
- •Пример. Методом Гаусса решить систему:
- •15. Однородные системы линейных уравнений.
- •16. Виды числовых множеств.
- •17. Понятия отображения и функции. Способы задания функции.
- •Понятие функции одной переменной
- •Способы задания функций:
- •Понятие функции одной переменной
- •Способы задания функций:
- •19. Понятия абсолютной величины. Свойства.
- •20. Монотонные и ограниченные функции. Четные и нечетные. Периодические функции. Сложная и обратная функции.
- •21. Предел функции х→∞и при х→х0. Односторонние пределы. Свойства пределов.
- •Свойства пределов функции
- •22. Числовые последовательности и их пределы. Свойства пределов.
- •23. Бесконечно малые величины. Сравнение бесконечно малых. Бесконечно малые величины
- •Связь бесконечно малых величин с пределами функций
- •Свойства бесконечно малых величин
- •Сравнение бесконечно малых
- •24. Замечательные пределы: число е. Следствия из 2-го замечательного предела. Второй замечательный предел.
- •25. Непрерывность функции. Точки разрыва 1-го и 2-го рода.
- •26. Понятие производной. Геометрический и механический смысл. Определение производной
- •27. Дифференцируемость и непрерывность.
- •28. Правила дифференцирования. Производная сложной функции. Производная линейной функции. Производная суммы, произведения, частного. Производная логарифма.
- •Основные правила дифференцирования
- •Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.Е.
- •5. Производная частного двух дифференцируемых функций может быть найдена по формуле
- •29. Правила дифференцирования. Производная от обратной функции. Производная степенной и показательной функции. Логарифмическое дифференцирование.
- •30. Правила дифференцирования. Производные тригонометрических и обратных тригонометрических функций.
- •Производная сложной функции
- •31. Дифференциал функции. Геометрический смысл. Свойства. Инвариантность формы.
- •Инвариантность формы дифференциала
- •32. Производные высших порядков.
- •33. Дифференциалы высших порядков.
- •34. Правило Лопиталя.
14. Методы Гаусса решения слау.
Метод Гаусса - метод последовательного исключения переменных.
Метод Гаусса заключается в том, что с помощью элементарных преобразований строк и перестановок столбцов система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Преобразования Гаусса удобно проводить не с самими уравнениями, а с расширенной матрицей их коэффициентов Ap, получаемой приписыванием к матрице A столбца свободных членов B:
![]() .
.
Следует отметить, что методом Гаусса можно решить любую систему уравнений вида .
Пример. Методом Гаусса решить систему:
![]()
Выпишем расширенную матрицу системы.
Шаг
1.
Поменяем
местами первую и вторую строки, чтобы
![]() стал равным 1.
стал равным 1.
Шаг 2. Умножим элементы первой строки на (–2) и (–1) и прибавим их к элементам второй и третьей строк, чтобы под элементом в первом столбце образовались нули.
Шаг 3. Умножим элементы третьей строки на (–0,5).
Шаг 4. Поменяем местами вторую и третью строки.
Шаг
5.
Поменяем
местами второй и третий столбец. (Шаги
3, 4, 5 приведены с тем, чтобы
![]() ).
).
Шаг
6. Элементы
второй строки умножим на 3 и прибавим
их к элементам третьей строки, тогда
под элементом
![]() появится нуль.
появится нуль.
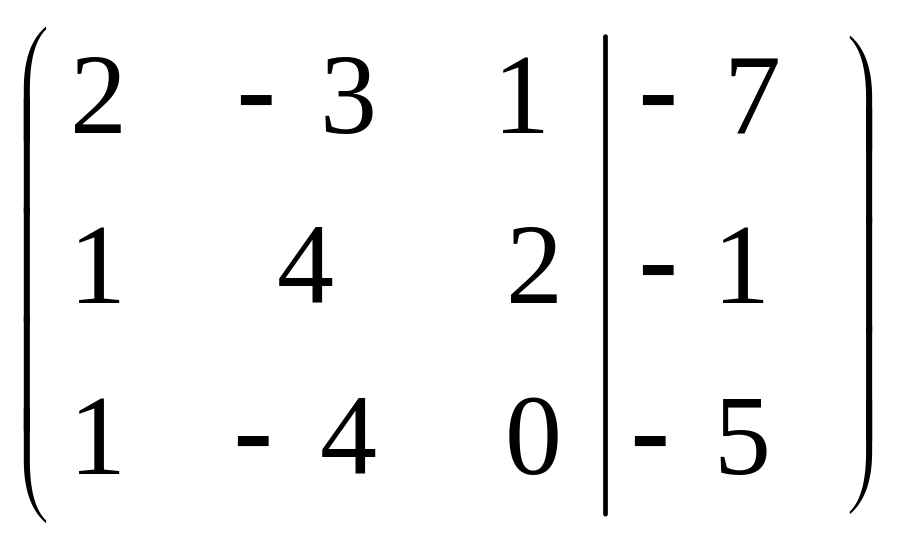 (называется
расширенная матрица системы)
(называется
расширенная матрица системы)
![]()
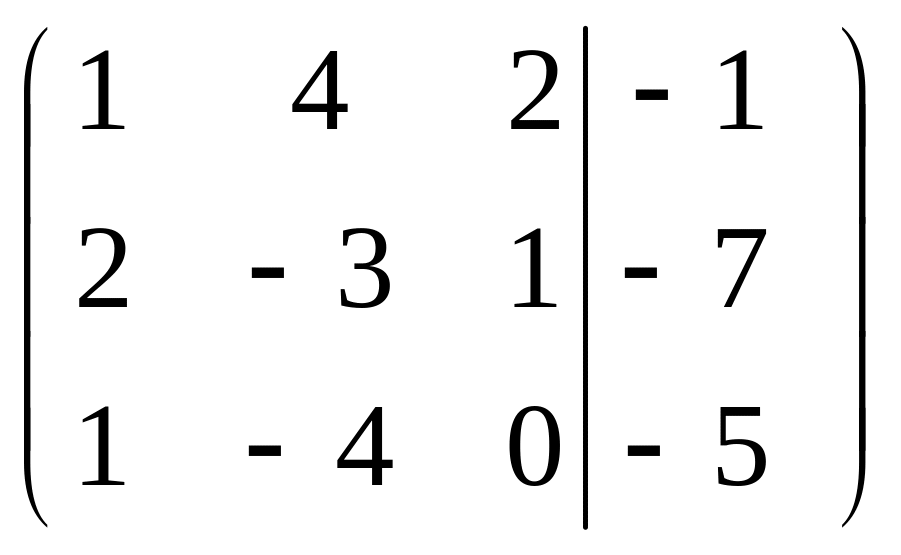
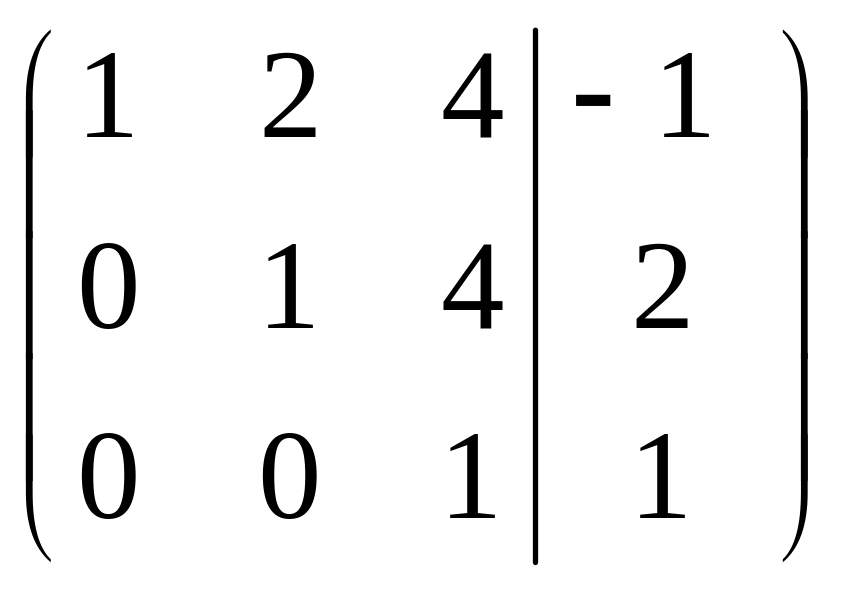 .
.
Расширенная матрица приведена к треугольному виду. Соответствующая ей система имеет вид:
![]()
Из
последнего уравнения
![]() ;
из второго
;
из второго
![]() ;
из первого
;
из первого
![]() .
.
Таким
образом,
![]() ,
,
,
,
![]() .
.
15. Однородные системы линейных уравнений.
Однородная сист всегда совместна, т.к. имеет след очевидн реш-я:
х1=0, все х = 0, все b=0
Опр 1: Реш-я, когда все х=0, назыв тривиальным или нулевым. Если есть хоть 1 реш-е, то оно ненулевое. Если r=n, след по теор 2 из бил 13 сущ единств реш-е
Теор 1: для того, чтобы однород слау имели не ноль решений, необх и дост чтобы ранг матр сист был меньше числа неизв
Теор 2: чтобы однород сист н-уравнений с н-неизв имела не ноль реш, необх и дост, чтобы опред = 0
Теор 3:если число Ур-ей в однород сист меньше числа неизв, значит сист имеет ненулев решения.
16. Виды числовых множеств.
N={1,2,3…} – мн-во натуральных чисел.
Z={…-3,-2,-1,0,1,2,3…}- мн-во целых чисел, N€Z.
Q=m/n, m€Z, n€N – рациональные числа, можно записать в виде дроби.
I={…пи, e, корень из двух, корень из трех, корень из пяти…} – мн-во иррациональн чисел ≠ m/n, m€Z, n€N
R1=R (мн-во действ чисел) – объед Q и I. (1) – указ на одномерное прост-во. Эл-ми явл отдельные числа.
Rn – мн-во, эл-ми котор являются упорядоч наборы из n-чисел. x€Х, х={ξ1, ξ2,… ξn}
Если n=2, то х={ξ1, ξ2 }, если n=3 – трехмерное прост-во {ξ1, ξ2, ξ3}.
При n>3, прост-во не имеет наглядн геометр представл-я.
17. Понятия отображения и функции. Способы задания функции.
Опр: Если в качестве х взято
