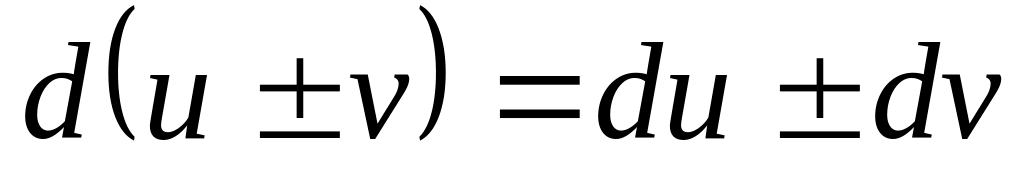29. Правила дифференцирования. Производная от обратной функции. Производная степенной и показательной функции. Логарифмическое дифференцирование.

1. Производная логарифмической функции.

А) . Воспользуемся схемой нахождения производных:

1) Дадим аргументу приращение и найдем наращение значений функции .

2) Находим приращение функции .

3) Составляем отношение .

4) Находим предел этого отношения при , т.е. .

Обозначив , найдем и .

В силу непрерывности логарифмической функции, используя 3 свойство функций непрерывных в точке. (Если функция непрерывна в точке , а функция непрерывна в точке , то сложная функция непрерывна в точке - ), меняем местами символы предела и логарифма, а затем используем определение числа ; получим:

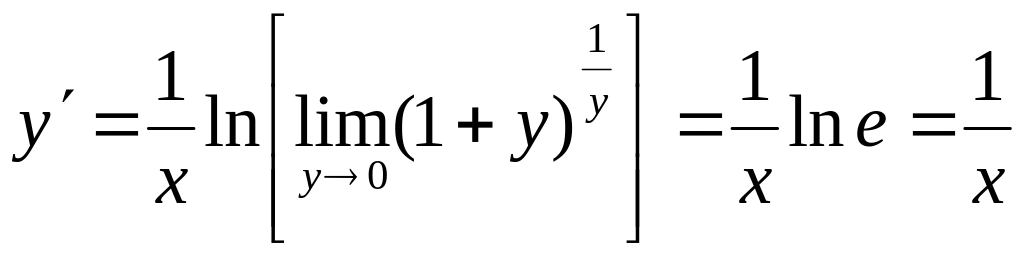. Итак, и .

Б) . Найдем , т.е.

и .

2. Производная показательной функции.

А) - прологарифмируем обе части равенства по основанию : . Дифференцируем или , откуда , т.е.

и .

Б) . . Итак,

и

3. Производная степенной функции.

, для любого . Прологарифмируем обе части равенства . Дифференцируем: , откуда , т.е:

и

4. Производная степенно-показательной функции.

. . Дифференцируем: .

30. Правила дифференцирования. Производные тригонометрических и обратных тригонометрических функций.

1. Производная тригонометрических функций.

и

и

и

и

Производная сложной функции

Пусть задана сложная функция .

Теорема. Если и - дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную промежуточного аргумента по независимой переменной , т.е.

.

□ Дадим независимой переменной х приращение Δх≠0. Тогда функция u= φ(x) и у=f(u) соответственно получат приращения Δu и Δy.

Предположим, что Δu≠0. Тогда в силу дифференцируемости функции у=f(u) можно записать где - f′(u) величина не зависящая от Δu.

На основании теоремы о связи бесконечно малых величин с пределами функций где - бесконечно малая величина при Δu → 0, откуда

Это равенство будет справедливо и при Δu = 0, если полагать, что α(∆u=0)=0 (т.е. доопределить таким образом функцию α(∆u) при ∆u=0).

Разделив обе части последнего равенства на Δх≠0, получим

Так как по условию функция у=φ(х) дифференцируема, то она непрерывна в точке х, следовательно, при Δх → 0 Δu → 0 и α(∆u) → 0 .

Поэтому, переходя к пределу при Δх → 0 в последнем соотношении, получаем ■

31. Дифференциал функции. Геометрический смысл. Свойства. Инвариантность формы.

Пусть функция определена на промежутке и дифференцируема в окрестности точки ,тогда или по теореме о связи бесконечно малых с пределами функций имеем , где - бесконечно малая величина при . Отсюда:

. ( 7.1)

Таким образом, приращение функции состоит из двух слагаемых:

1) - линейного относительно , т.к. ;

2) - нелинейного относительно , т.к. .

Определение. Дифференциалом функции называется главная, линейная относительно часть приращения функции, равная произведению производной на приращение независимой переменной:

. ( 7.2)

Пример. Найти приращение функции при и :

Решение. ,

Пример. Найти дифференциал функции .

Решение. По формуле (7.2.) имеем .

Определение. Дифференциал независимой переменной равен приращению этой переменной:

( 7.3)

Тогда формулу (7.2) для дифференциала функции можно записать в виде:

( 7.4)

Откуда , поэтому можно рассматривать не только как символическое обозначение производной, но и как обычную дробь с числителем и знаменателем .

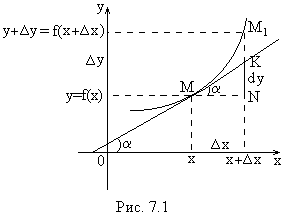
Геометрический смысл. На графике функции (рис. 7.1.) возьмем произвольную точку . Дадим аргументу приращение , тогда функция получает приращение . В точке проведем касательную, образующую угол с осью . Из треугольника : . Из имеем: . Таким образом, и соответствует формуле (7.1).

Следовательно, с геометрической точки зрения дифференциал функции есть приращение ординаты касательной, проведенной к графику функции в данной точке, когда получает приращение .

Свойства дифференциала аналогичны свойствам производной.

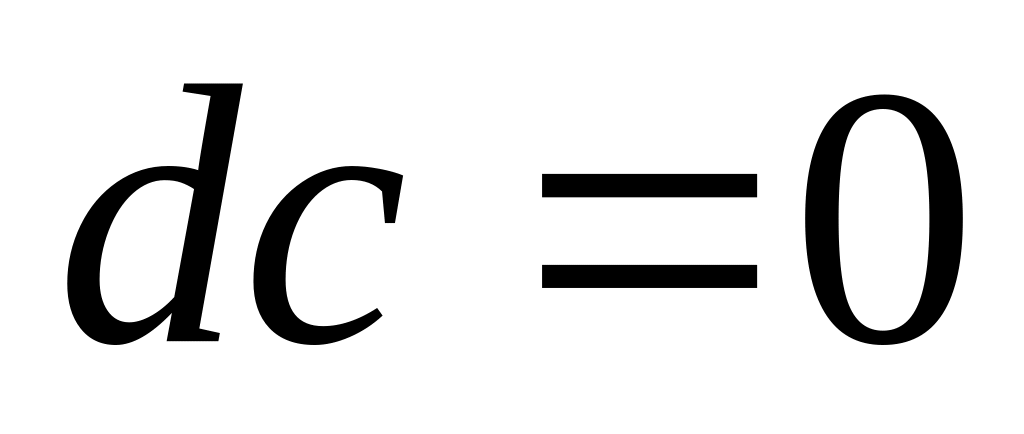
1)	4)
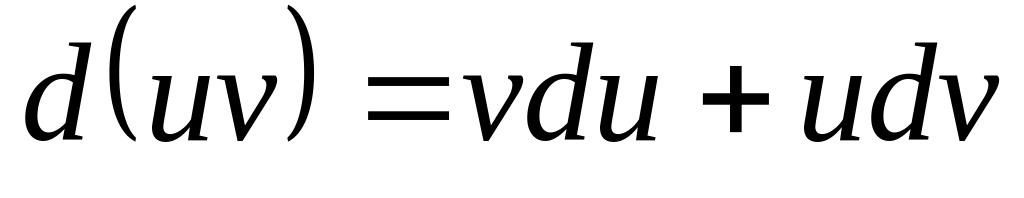
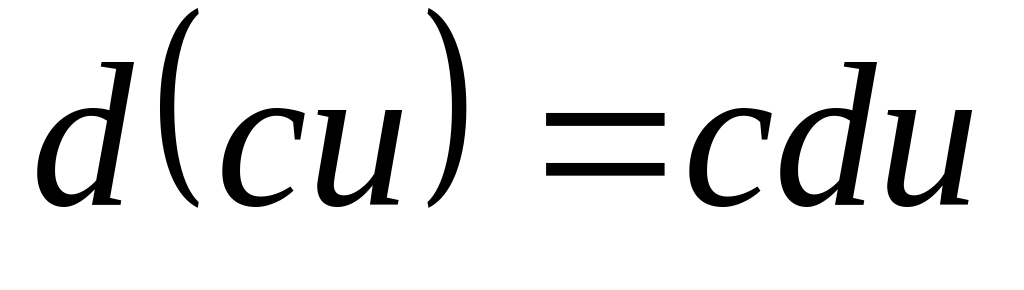
2)	5)
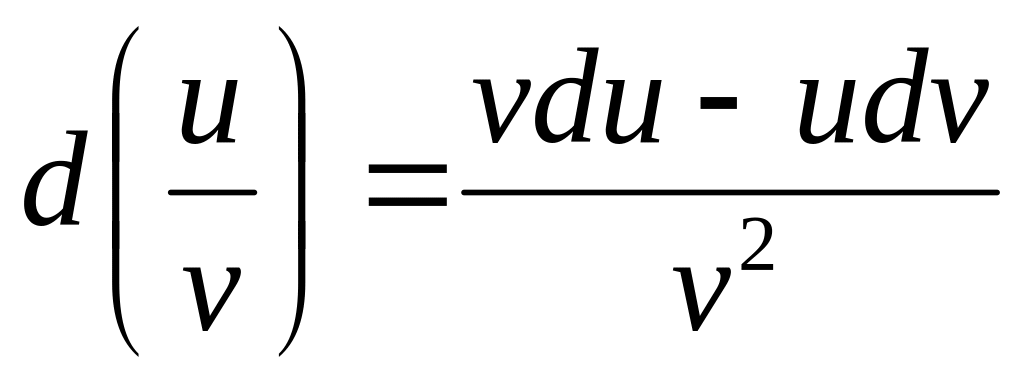
3)