Вопрос 9.

Определение выигрыш-функции в смешанных стратегиях; координатные и векторно-матричные формулы ее представления.

Функция H(P,Q)= ,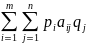

Определённая на декартовом произведении S_A × S_B множеств смешанных стратегий S_A и S_B соответственно игроков А и В и ставящая в соответствие каждой ситуации (P,Q) ϵ S_A × S_B в смешанных стратегиях Р=(р₁, р₂,…, р_m) игрока А и Q=(q₁, q₂,…, q_n) игрока В средневзвешенный выигрыш игрока А в этой ситуации, определяемый выражением в правой части равенства H(P,Q)= , называется выигрыш-функцией игрока А в смешанных стратегиях.

Сужение выигрыш-функции Н на декартово произведении S^C_A × S^C_B множеств чистых стратегий S^C_A и S^C_B совпадает с выигрыш-функцией F в чистых стратегиях, т.е. H(A_i, B_j)=F(A_i, B_j)=a_ij, i=1,2, …, m; j=1,2,…,n. Поэтому совокупность 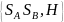множеств смешанных стратегий S_A и S_B игроков А и В и выигрыш-функции игрока А в смешанных стратегиях Н называется смешанным расширением игры 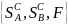в чистых стратегиях.

Выигрыш-функцию в смешанных стратегиях, заданную в координатной форме H(P,Q)= , можно представить и в матричной форме:

Р(P,Q)=PAQ^T,

Где Р=(р₁, р₂,…, р_m) – вектор-строка смешанной стратегии игрока А размера [1×m]; А – матрица выигрышей игрока А в чистых стратегиях размера [m×n]; Q^T=(q₁, q₂,…, q_n)^T – вектор-столбец размера [n×1] смешанной стратегии игрока В.

Вопрос 10.

Определения нижней и верхней цен игры в смешанных стратегиях и их

существование.

Нижней ценой, или максимином, в матричной игры в смешанных стратегиях называется величина =

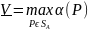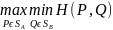
Верхней ценой, или минимаксом, матричной игры в смешанных стратегиях называется величина

=

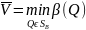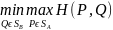
Теорема. Для любой конечной матричной игры существует нижняя и верхняя цены игры в смешанных стратегиях.

Смешанная стратегия P^o ϵ S_A , максимизирующая показатель эффективности , называется максиминной смешанной стратегией игрока А. Таким образом, =α(P^o). Множество всех максиминных смешанных стратегий игрока А обозначим через (S_A)^maxmin .

Смешанная стратегия Q^o ϵS_B , минимизирующая показатель неэффективности β(Q), называется минимаксной смешанной стратегией игрока В. Таким образом, 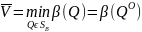. Множество всех минимаксных смешанных стратегий игрока В обозначим через (S_B)^minmax.

Нижняя цена игры α и верхняя цена игры β в чистых стратегиях, нижняя цена игры 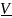и верхняя цена игры 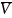в смешанных стратегиях удовлетворяют следующим неравенствам

α≤ ≤ ≤β

Теорема

Для любой конечной матричной игры существуют нижняя и верхняя цены игры в смешанных стратегиях.

Доказательство:

Так как функция α(Р) непрерывна на компакте S_A, то она достигает на этом множестве своего максимума, т.е. существует нижняя цена игры в смешанных стратегиях:

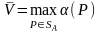
Аналогичным образом обосновывается существование и верхней цены игры в смешанных стратегиях.

11. Критерий существования седловых точек

Седловым элементом матрицы называется элемент, являющийся минимальным в своей строке и максимальным в своем столбце.

Ситуацию (s*, t*) назовем седловой точкой игры  = <S, T, >, если

 sS  tT ( s, t*)  ( s*, t*)  ( s*, t). (3)

Теорема 2 (критерий существования седловой точки).

Для того, чтобы матричная игра  = <S, T, > имела седловые точки необходимо и достаточно, чтобы были равны величины  и .

Доказательство.

Необходимость.

Пусть (s*, t*) – седловая точка, т. е. выполнено (3).

1. Так как ( s_i, t*)  ( s*, t*), а ( s*, t*) – число, то

,

а отсюда следует (берем минимум по j, от которого левая часть не зависит), что

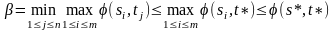(4)

2. Так как ( s*, t*)  ( s*, t_j), а ( s*, t*) – число, то

,

а отсюда следует, что

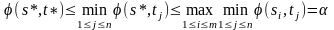(5)

3. Объединяя (4) и (5), получаем   ( s*, t*)  .

Поскольку по теореме о минимаксе и максимине   , то  = .

Замечание 1.

В равенстве (3) s* и t* максиминная и минимаксная стратегии соответственно.

Достаточность.

Пусть выполнено  = , т. е. .

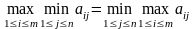Обозначим

s*S : ,

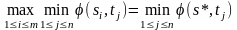t*T : .

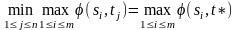Докажем, что (s*, t*) – седловая точка.

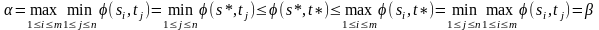
(а) (б)

Поскольку  = , то в последней цепочке все неравенства выполняются в виде равенств. Следовательно, получаем:

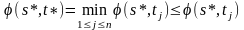
Из (а):  j

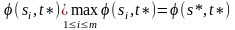
Из (б):  i

Последние два неравенства и дают (3).

Теорема доказана.