
- •Понятие генеральной совокупности и выборки. Эмпирические аналоги параметров генеральной совокупности. Два взгляда на выборку. Вероятностные свойства выборочных характеристик.
- •Выборочные моменты. Вывести формулы, устанавливающие связь между центральными и начальными выборочными моментами для
- •6. Достаточность точечной оценки. Критерий факторизации. Доказать достаточность средней арифметической , используемой в качестве оценки параметра λ пуассоновского закона распределения .
- •8. Точные и асимптотические законы распределения выборочных характеристик. Вывести закон распределения в предположении, что выборка взята из нормальной генеральной совокупности х.
- •9. Вывести закон распределения ( ) в предположении, что выборки независимы и взяты из нормальных генеральных совокупностей х и у.
- •10. Доказать, что статистика имеет - распределение с (n-1) степенями свободы.
- •11. Доказать, что статистики и s2 , полученные по выборке из нормальной генеральной совокупности, независимы.
- •12. Случайная величина и статистики, имеющие -распределение. Их применение при оценивании параметров и проверке гипотез.
- •13. Случайная величина и статистики, имеющие t-распределение Стьюдента. Их применение в задачах оценивания параметров и проверке гипотез.
- •14. Случайная величина и статистики, имеющие f-распределение, и их применение в математической статистике.
- •16. Интервальные оценки для генеральной дисперсии, полученные по выборке из нормальной генеральной совокупности.
- •19. Проверка гипотез о значении генеральной средней, при известной и неизвестной генеральной дисперсии. Вычисление мощности критерия.
- •20. Проверка гипотез о равенстве генеральных средних двух нормальных генеральных совокупностей. ( это без лекций)
- •21. Проблема Беренса - Фишера. Сравнение математических ожиданий двух нормальных генеральных совокупностей, генеральные дисперсии которых неизвестны и не равны.
- •22. Проверка предположения, что две выборки объемом n1 и n2 взяты из одной нормальной генеральной совокупности.
- •23. Проверка гипотез о значении дисперсии генеральной совокупности. Вычисление мощности критерия (Без вывода мощности)
- •24. Проверка гипотез об однородности дисперсий ряда генеральных совокупностей. Критерии Бартлетта и Кохрана.
- •Проверка гипотезы однородности ряда вероятностей в случае биноминального распределения.
- •Проверка гипотезы однородности ряда вероятностей в случае полиномиального распределения.
- •27.Однофакторный дисперсионный анализ и его цель. Разложение общей вариации на составляющие. Общий вид модели.
- •28.Модель м1 однофакторного дисперсионного анализа. Проверка гипотезы о влиянии фактора а на результативный признак у. Вывести статистику критерия.
- •29. Модель м2 однофакторного дисперсионного анализа. Проверка гипотезы о влиянии фактора а на результативный признак у. Вывести статистику критерия.(нет)
- •30. Модель м1 однофакторного дисперсионного анализа. Проверка гипотезы относительно общего среднего. Вывести статистику критерия.
- •32. Модель м2 однофакторного дисперсионного анализа. Проверка гипотезы относительно общего среднего. Вывести статистику критерия.
- •33. Двухфакторный дисперсионный анализ и его цель. Разложение общей вариации на составляющие. Особенности моделей м1, м2 и смешанных.
23. Проверка гипотез о значении дисперсии генеральной совокупности. Вычисление мощности критерия (Без вывода мощности)
Пусть
из генеральной совокупности, значения
признака которой распределены по НЗР
с неизвестной дисперсией
,
взята случайная выборка из n
независимых наблюдений и пусть S2
–
выборочная дисперсия. Требуется
проверить нулевую гипотезу H0
: ,
где
,
где
 - определенное заданное значение
дисперсии. Используют выборочную
характеристику:
- определенное заданное значение
дисперсии. Используют выборочную
характеристику:
 ,
которая при выполнении гипотезы H0
имеет
распределение «хи-квадрат» с (n-1)
степенями
свободы.
,
которая при выполнении гипотезы H0
имеет
распределение «хи-квадрат» с (n-1)
степенями
свободы.
Критические области выбираются исходя из конкурирующей гипотезы:
H1:
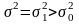 -
ПКО =>
-
ПКО =>

Если
 , то нулевую гипотезу отвергают. Если
, то нулевую гипотезу отвергают. Если
 ,
то гипотеза не противоречит опытным
данным.
,
то гипотеза не противоречит опытным
данным.
Мощность
критерия в этом случае:

H1:
 -
ЛКО =>
-
ЛКО =>

Если
 ,
то гипотеза отвергается. Если
,
то гипотеза отвергается. Если
 - не отвергается.
- не отвергается.
Мощность
критерия:

H1:
 => ДКО => Левую и правую границы
критической области находят из условий:
=> ДКО => Левую и правую границы
критической области находят из условий:
 и
и

Если
 => гипотеза не отвергается
=> гипотеза не отвергается
Если
 и
и
 => отвергается
=> отвергается
24. Проверка гипотез об однородности дисперсий ряда генеральных совокупностей. Критерии Бартлетта и Кохрана.
Критерий
Бартлетта Пусть
Х1,
Х2
,…,
Хl
– l
нормал.
генер. сов., из котор. извлечены выборки
объемом
 ;
;
 –
исправ. выбор. дисперсии.
–
исправ. выбор. дисперсии.
На
уровне знач.
провер. нулев. гип. о рав-ве дисп. l
генер. сов., т.е.
 .
.
 – число степ. свободы i-й
выборки;
– число степ. свободы i-й
выборки;
 для
для
 ,
где
,
где
 – результат j-го
набл. для i-й
выборки;
– результат j-го
набл. для i-й
выборки;
 .
.
Выбороч.
х-ка критерия: ,
где
,
где
 .
.
При
выполн. нулев. гип. Н0
и при
 ,
,
 приближенно имеет распред.
с
l-1
степ. свободы.
приближенно имеет распред.
с
l-1
степ. свободы.
Для
проверки нулев. гип. строят правостор.
крит. обл., границу котор. опред. по табл.
распределения
для уров. знач.
и числа степ. свободы
 из условия:
из условия:
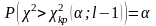 .
.
Критерий
проверки: если
 ,
то гипотезу отвергают, если же
,
то гипотезу отвергают, если же
 ,
то считают, что гипотеза не противоречит
опытным данным.
,
то считают, что гипотеза не противоречит
опытным данным.
Критерий Бартлетта весьма чувствителен к отклонениям законов распред. Хi для от норм. закона.
Критерий
Кохрана Пусть
Х1,
Х2
,…,
Хl
– l
нормал.
генер. сов., из котор. извлечены незав.
случ. выборки одинак. объема
 ;
–
исправ. выбор. дисперсии.
;
–
исправ. выбор. дисперсии.
На уровне знач. провер. нулев. гип. о рав-ве дисп. l генер. сов., т.е. .
Выбороч. х-ка критерия:
 ,
котор. при выпол. нулев. гип. имеет
G-распределение
с
,
котор. при выпол. нулев. гип. имеет
G-распределение
с
 и
и
 ,
где
,
где
 –
наибольш. из исправ. выбор. диспер. Для
проверки нулев. гип. строят правостор.
крит. обл., границу котор. опред. по табл.
G-распределения
из условия:
–
наибольш. из исправ. выбор. диспер. Для
проверки нулев. гип. строят правостор.
крит. обл., границу котор. опред. по табл.
G-распределения
из условия:
 .
.
Критерий
проверки: если
 ,
то гипотезу отвергают, если же
,
то гипотезу отвергают, если же
 ,
то считают, что гипотеза не противоречит
опытным данным.
,
то считают, что гипотеза не противоречит
опытным данным.
Проверка гипотезы однородности ряда вероятностей в случае биноминального распределения.
Пусть Х1, Х2 ,…, Хl – lгенер. сов., каждая из котор. характериз. неизв. параметром Pi, где Pi–вероят. появл. события А в соотв. выборке.
Требуется
провер. нулев. гип. о рав-ве вероят.
появлен. события А в генер. совокупностях,
т.е.
 .
.
Для проверки гип.использ. статистику:
 ,
где
,
где
 – средн. частость появлен. события А
по всем выборкам.
– средн. частость появлен. события А
по всем выборкам.
Или,
используя частости по всем выборкам
 :
:
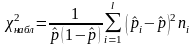 .
.
Статистика при выполн. нулев. гип.имеет асимптотическое распред. с l-1 степ. свободы, где l– число генер. совокуп.
Для проверки нулев. гип.на уров. знач. строят правостор. крит. обл., границу котор. опред. из условия:
.
Критерий проверки: если , то гипотезу отвергают, если же , то считают, что гипотеза не противоречит опытным данным.
