21. Проблема Беренса - Фишера. Сравнение математических ожиданий двух нормальных генеральных совокупностей, генеральные дисперсии которых неизвестны и не равны.

Проблема Беренса-Фишера- аналитическая проблема, возникшая в связи со стат. задачей сравнения по эмпирическим данным мат. ожиданий в двух нормальных распределениях, дисперсии кот-ых неизвестны (предполагается, что отношение дисперсий также неизвестно).

Х ϵ N( ; ₎ => => ,

Y ϵ N( ; ₎ => => ,

Выборки независимы.

Проверим гипотезу : 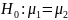, без предположения равенства

Эта статистика (2) имеет t-распределение Стьюдента с числом степ.своб

,

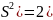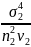= , т.к. несмещенная оценка D( – по определению D( ) = D( D( + ) (3)

Апроксимизируем распр. распределением некой статистики 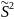с степенью свободы

Условия

1. 

D( + ) (4)

Решаем (3)=(4) относительно , получаем. Число степеней свободы высчитывается по формуле:

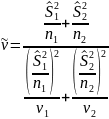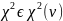(5) (заменили на их несмещенные оценки) Надо показать, что (5) имеет t-распределение (6), Z , , (7)

Тогда, учитывая (6), и подставив в него (1) и (7), будем иметь

Из следующей формулы определяется критическая область.

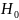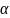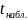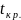отвергается с вероятностью ошибки , если > => . В противном случае гипотеза не отвергается.

22. Проверка предположения, что две выборки объемом n1 и n2 взяты из одной нормальной генеральной совокупности.

Для проверки того, что выборки взяты из одной генеральной совокупности, необходимо проверить гипотезу о равенстве генеральных средних двух выборок и гипотезу о равенстве дисперсий.

Из генеральных совокупностей взяты две независимые выборки объемом и . Пусть и - средние арифметические выборочных совокупностей. Для проверки гипотезы H₀ : использую статистику:

Которая при выполнении нулевой гипотезы имеет нормированный нормальный закон распределения.

При H₁: => ПКО => H₁: => ЛКО => H₁: => ДКО => Тогда, если: => отвергается с вероятностью ошибки => не противоречит опытным данным

Пусть Х и У – генеральные совокупности, значения признаков которых распределены по нормальному закону с дисперсиями и . Из этих совокупностей взяты две случайные независимые выборки, объемами n_x и n_y , и пусть и - исправленные выборочные дисперсии,

причем , где Требуется проверить H₀ : против альтернативной H₁ : . Основой критерия является статистика: , которая при выполнении нулевой гипотезы имеет распределение Фишера-Снедекора(F-распределение) с и степенями свободы.

Для проверки выбирают ПКО. Границу критической области определяют из условия:

Если => гипотеза не противоречит опытным данным Если => гипотеза отвергается

Пусть X и Y нормальные совокупности с равными, но неизвестными дисперсиями и математическими ожиданиями и . Из этих совокупностей взяты две случайные независимые выборки с параметрами , и , . На уровне значимости проверяется гипотеза H₀ : . В основе критерия лежит статистика:

Которая при выполнении нулевой гипотезы H₀ имеет распределение Стьюдента с степенями свободы. При заданном уровне значимости выбор критической области зависит от конкурирующей гипотезы:

H₁: - ПКО или H₁: -ЛКО => H₁: ДКО =>

Тогда, если: => отвергается с вероятностью ошибки => не противоречит опытным данным