9. Вывести закон распределения ( ) в предположении, что выборки независимы и взяты из нормальных генеральных совокупностей х и у.

Если – выборка объемом n₁ из нормальной ген. сов. X € N(μ1;σ1), – выборка объемом 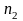из нормальной ген. сов. Y € N(μ2;σ2), причем выборки независимы, то Z=

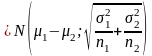
Производящая функция

Т.к. произв. Ф-я суммы равна произведению производ. Ф-й слагаемых, то

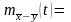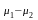* M(z)= D(z)=

10. Доказать, что статистика имеет - распределение с (n-1) степенями свободы.

Если – случайная выборка объемом n из X € N(μ;σ), то

статистика 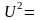имеет - распределение с (n-1) степенями свободы

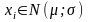Доказательство: Не нарушая общности, будем предполагать, что Х-центрированная величина X € N(0;σ) , X=x’- μ, причем Перейдем от СВ i=1,N к новой системе СВ , j=1,N

(1)

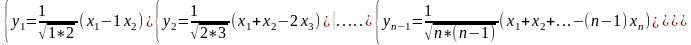(2)

Составим матрицу А коэффициентов преобразования

А=

Покажем, что матрица А удовлетворяет ортогональности:

1. 

2. Сумма произв. соответствующих 2-х строк или 2-х стобл=0

Таким образом, с помощью ортогональной матрицы А ( ) ) преобразуется в

Ортогональным называется n-мерное преобразование ЛП, сохраняющее длину каждого вектора.

Из (2) и

,

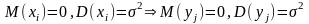
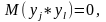
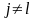=> Yj-взаимно некоррел.

нормированных нормальных величин

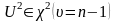
11. Доказать, что статистики и s2 , полученные по выборке из нормальной генеральной совокупности, независимы.

Если – случайная выборка объемом n из X € N(μ;σ), то

статистика имеет - распределение с (n-1) степенями свободы.

Доказательство: Не нарушая общности, будем предполагать, что Х-центрированная величина X € N(0;σ) , X=x’- μ, причем Перейдем от СВ i=1,N к новой системе СВ , j=1,N

(1)

(2)

Составим матрицу А коэффициентов преобразования

А=

Покажем, что матрица А удовлетворяет ортогональности:

2. Сумма произв. соответствующих 2-х строк или 2-х стобл=0

Таким образом, с помощью ортогональной матрицы А ( ) ) преобразуется в

Ортогональным называется n-мерное преобразование ЛП, сохраняющее длину каждого вектора.

Из (2) и

,

=> Yj-взаимно некоррел.

нормированных нормальных величин

,

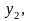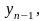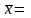
Так как … и независимы между собой, тогда независимы и величины и =

12. Случайная величина и статистики, имеющие -распределение. Их применение при оценивании параметров и проверке гипотез.

Если (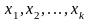 )-взаимно независимые СВ, имеющие нормированные нормальный ЗР , тогда 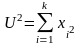имеет распределение с числом степеней свободы 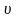=k. , где k-число нез. слагаемых.

Свойства:1) Если и 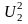- есть независим. СВ, имеющие -распределение со степен свободы к1 и к2, то +

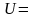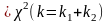
При СВ Из определения СВ => 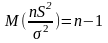, , Bn= - = при _n-беск

=> - состоятельная

Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений. Критерий согласия Пирсона - χ² – критерий проверки гипотезы о том, что изучаемая случайная величина подчиняется заданному закону распределения: H₀: F(x) = F₀(x).

Наблюдаемое значение статистики критерия рассчитывается на основе данных, представленных в виде вариационного ряда по формуле: 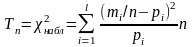,где m_i – частота i-го значения или интервала (число наблюдений выборки, равных i-му значению x_i, или попадающих в i-й интервал (a_i; b_i), i = 1, … , l;

p_i – вероятность принятия случайной величиной i-го значения или вероятность попадания в i-й интервал;

n – объем выборки n = Σ m_i. Часто для расчетов вводят понятие "теоретической частоты" m_i^T = np_i, что позволяет преобразовать формулу наблюдаемого значения статистики критерия к виду: ,

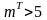
По теореме Пирсона при истинности гипотезы H₀ и n → ∞, распределение статистики χ²_набл сходится к χ²-распределению с ν = l – r – 1 степенями свободы, где r - число параметров предполагаемого теоретического зако­на, использованных для вычисления теоретических частот и оценива­емых по выборке. Для проверки нулевой гипотезы H₀ на уровне значимости α строят ПКО. P(χ² > χ²_кр(α; l – r – 1)) = α. Гипотеза отвергается на уровне значимости , если вычисленное значение χ²_набл окажется больше критического χ²_кр(α,ν), найденного по таблицам распределения χ² для уровня значимости  и числа степеней свободы ν = l – r - 1. В противном случае гипотеза не отвергается.

1. Применяется при построении доверительного интервала с заданной надежностью γ для генеральной дисперсии σ² при малых объемах выборки (n≤30).

2. Применяется при проверке гипотезы о значении генеральной дисперсии при нахождении критической области.

3. Применяется при проверке гипотез об однородности ряда дисперсий (Критерий Бартлетта) при нахождении критической области.

4. Применяется при проверке гипотез об однородности ряда вероятностей для биномиального закона распределения (n>30) при нахождении критической области.

5. Применяется при проверке гипотез об однородностей ряда вероятностей в случае полиномиального распределения при нахождении критической области.

6. Применяется при использовании критерия согласия Пирсона.

7. Применяется при нахождении интервальной оценки для остаточной дисперсии σ² с заданной надежностью γ (дисперсионный анализ и однофакторный, и двухфакторный).