Интерференция в тонких пленках, оптическая длина волны, оптическая разность хода лучей.

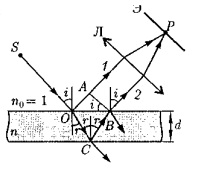
В природе часто можно наблюдать радужное окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри), возникающее в результате интерференции света, отраженного двумя поверхностями пленки. Пусть на плоскопараллельную прозрачную пленку с показателем преломления п и толщиной d под углом i падает плоская монохроматическая волна (для простоты рассмотрим один луч). На поверхности пленки в точке О луч разделится на два: частично отразится от верхней поверхности пленки, а частично преломится. Преломленный луч, дойдя до точки С, частично преломится в воздух (n_о = 1), а частично отразится и пойдет к точке В. Здесь он опять частично отразится (этот ход луча в дальнейшем из-за малой интенсивности не рассматриваем) и преломится, выходя в воздух под углом i. Вышедшие из пленки лучи 1 и 2 когерентны, если оптическая разность их хода мала по сравнению с длиной когерентности падающей волны. Если на их пути поставить собирающую линзу, то они сойдутся в одной из точек Р фокальной плоскости линзы и дадут интерференционную картину, которая определяется оптической разностью хода между интерферирующими лучами. Оптическая разность хода, возникающая между двумя интерферирующими лучами от точки О до плоскости АВ,

∆ = n(ОС+СВ)-(ОА± λ/2),

где показатель преломления окружающей пленку среды принят равным 1, а член ±λ/2 обусловлен потерей полуволны при отражении света от границы раздела. Если n>n_о, то потеря полуволны произойдет в точке О и вышеупомянутый член будет иметь знак минус, если же n<n_о, то потеря полуволны произойдет в точке С и λ/2 будет иметь знак плюс. OC=CB = d/cos(r)

OA=OB*sin(i) = 2d tg r sin i.

Учитывая для данного случая закон преломления sin(i) = n sin г, получим

О птическая длина пути - произведение расстояния, которое проходит свет и показателя преломления среды, в которой этот свет идет. Смысл этого понятия состоит в том, что, проходя через среду с показателем преломления большим единицы, свет запаздывает (т. е. как будто бы проходит больший путь) по отношению к свету, который шел бы то же расстояние в среде с n=1. Оптическая разность хода - разность между оптическими длинами путей, по которым проходит свет. Так как сравниваются произведения, то эта разность может вызываться как разницей показателей преломления, так и разницей расстояний. С другой стороны, показатели преломления и расстояния могут быть такими, что, будучи разными, они обеспечат разность хода, равную нулю.

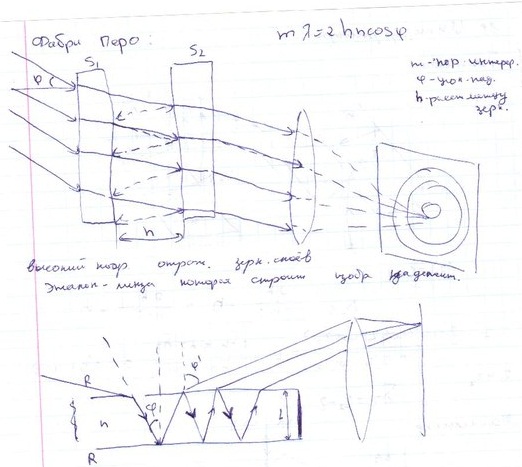
Интерферометры: Томпсона, Майкельсона, эталон Фабри-Перо, пластинка Люммера-Герке.

Д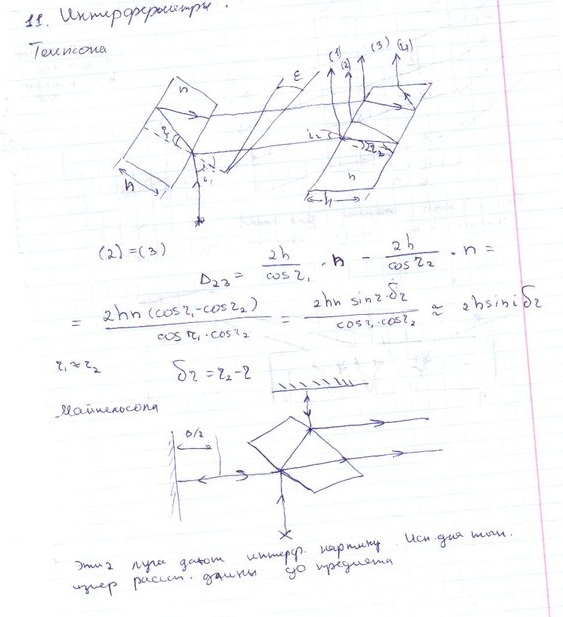 ифракция. Принцип Гюйгенса, принцип Гюйгенса-Френеля. Метод зон Френеля для сферических и плоских волн. Зонные пластинки, графическое представление ( спираль Корню).

Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле — любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Явление дифракции объясняется с помощью принципа Гюйгенса согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий

момент времени.

П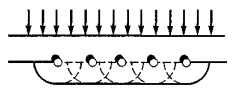 ринцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а следовательно, и об интенсивности волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.

Согласно принципу Гюйгенса —Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками.

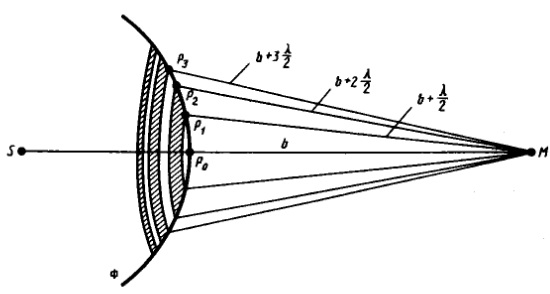
Принцип Гюйгенса — Френеля в рамках волновой теории должен был ответить на вопрос о прямолинейном распространении света. Френель решил эту задачу, рассмотрев взаимную интерференцию вторичных волн и применив прием, получивший название метода зон Френеля. Найдем в произвольной точке М амплитуду световой волны, распространяющейся в однородной среде из точечного источника S. Согласно принципу Гюйгенса — Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Ф, являющейся поверхностью фронта волны, идущей из

S (поверхность сферы с центром S). Френель разбил волновую поверхность Ф на кольцевые зоны такого размера, чтобы расстояния от краев зоны до М отличались на λ/2. Подобное

разбиение фронта волны на зоны можно выполнить, проведя с центром в точке М

сферы радиусами b+λ/2 , b+2*λ/2 ...

Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на λ/2, то в точку М они приходят в противоположной фазе и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания

в точке М

А=А1-А2+А3-А4 + ...±Аm, 177.1

где Am — амплитуда колебания, возбуждаемых m-й зоной. Для оценки амплитуд колебаний найдем площади зон Френеля.

В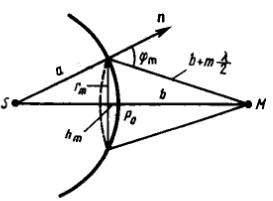 нешняя граница m-й зоны выделяет на волновой поверхности сферический сегмент высоты h_m. Обозначив площадь этого сегмента через P, найдем, что площадь m-й зоны Френеля равна

∆ P=Pm-P_m-1

где P_m-1— площадь сферического сегмента, выделяемого внешней границей (m—1)-й зоны.

Из рисунка следует, что

177,2

После элементарных преобразований, учитывая что λ<<a и λ<<b получим

В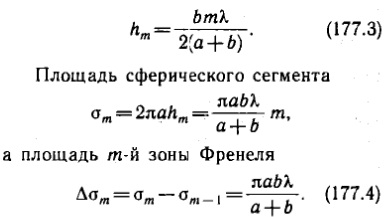 ыражение 177.4 не зависит от m; следовательно, при не слишком больших m площади зон Френеля одинаковы. Таким образом, построение зон Френеля разбивает волновую поверхность сферической волны на равные зоны. Согласно предположению Френеля,

действие отдельных зон в точке М тем меньше, чем больше угол ф_m между нормалью n к поверхности зоны и направлением на М, т. е. действие зон постепенно убывает от центральной к периферическим. Кроме того, интенсивность излучения в направлении точки М уменьшается с ростом m и вследствие увеличения расстояния от зоны до точки М. Учитывая оба этих фактора, можем записать

A1>A2>...

Общее число зон Френеля, умещающихся на полусфере, очень велико; Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания Ат от некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон

т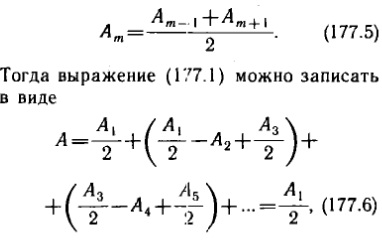 ак как выражения, стоящие в скобках равны нулю, а оставшаяся часть от амплитуды последней зоны ±Аm/2 ничтожно мала. Если в выражении 177.2 положим, что высота сегмента h_m<<а (при не слишком больших m), тогда r² = 2ah_m. Подставив сюда значение 177,3, найдем радиус внешней границы т-й зоны Френеля:

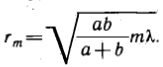П равомерность деления волнового фронта на зоны Френеля подтверждена кспериментально. Для этого используются зонные пластинки — в простейшем случае стеклянные пластинки, состоящие из системы чередующихся прозрачных и непрозрачных концентрических колец, построенных по принципу расположения зон Френеля, т. е. с радиусами зон Френеля,

для определенных значений а, Ь и λ (m = 0,2,4, ... для прозрачных и ш=1, 3, 5, ... для непрозрачных колец). Если поместить зонную пластинку на расстоянии а от точечного источника и на расстоянии b от точки наблюдения на линии, соединяющей эти две точки, то для света длиной волны λ она перекроет четные зоны и оставит свободными нечетные начиная с центральной. В результате этого результирующая амплитуда должна быть больше, чем при полностью открытом фронте. Действительно, на опыте зонная пластинка во много раз увеличивает интенсивность света в точке М, действуя подобно собирающей линзе.