Примеры множества Евклидова пространства Em:

1)Множество точек определяемых неравенством: ρ²(M₀,M)=(x₁-x₁₀)²+(x₂-x₂₀)²+…+(x_m-x_m0)²≤R² называется m-мерным шаром, радиуса R с центром в точке M₀.

Множество, определяемое неравенством ρ(M₀,M)<R называется открытым m-мерным шаром.

Множество, определяемое неравенством ρ(M₀,M)=R называется m-мерной сферой.

2)Множество точек, определенных неравенствами:

|x₁-x₁₀|<d_1, |x₂-x₂₀|<d₂,…, |x_m-x_m0|<d_m называется открытым m-мерным параллелепипедом.

3)έ-окрестность точки M₀ открытым m-мерным шаром радиуса έ с центром в точке M₀.

Понятие функции многих переменных: Определение: Считается, что на множестве {M} пространства E^m задана функция многих переменных U=f(M)=f(x₁,x₂,..,x_m). Если каждой точке M {M} ставится в соответствие по известному закону число U из множества {U}. Множество {M} называется областью значения или областью определения функции f(M). Множество {U} называется множеством значения функции.

Последовательность точек (сходимость, ограниченность): Определение: Последовательность {M_n} точек пространства E^m называется сходящейся к точке M₀, если для любой έ>0 найдется номер N такое, что при n≥N выполняется неравенство: ρ(M₀,M_n)< έ. Определение: Последовательность {M_n} точек пространства E^m называется ограниченной, если существует число A >0 такое, что для всех номеров n выполняется неравенство ρ(0,M_n)≤A, где 0-точка, все координаты которой равны 0. Определение: Последовательность {M_n} точек пространства E^m называется фундаментальной, если для любого έ>0 найдется номер N такой, что при n≥N и любом натуральном p выполняется неравенство ρ(M_n,M_n+p)< έ.

Критерий Коши. Для того, чтобы последовательность {M_n} точек пространства была сходящейся, необходимо и достаточно, чтобы она была фундаментальной.

Предельное значение функции многих переменных.

1-е определение. Число b называется предельным значением функции f(M) в точке M₀ последовательности {M_n} точек множества {M} соответствующая последовательность значений функции f(M1),f(M2),…,f(M_n) сходится к числу b.

2-е определение. Число b называется предельным значением функции f(M) в точке M₀, если для любого έ>0 найдется число б>0 такое, что при выполнении условия 0< ρ(M₀,M_n)<б выполняется неравенство |f(M_n)-b|< έ.

Критерий существования предельного значения функции. Считается, что функция U=f(M) удовлетворяет в т. M₀ условию Коши, если для любого έ>0 найдется число б>0 такое, что для любой пары точек M’,M’’ {M} и удовлетворяющих неравенствам 0< ρ(M₀,M’)<б , 0< ρ(M₀,M’’)<б выполняется неравенство |f(M’’)-f(M’)|< έ.

Для того, чтобы у функции f(M) существовало предельное значение в т.M₀ необходимо и достаточно, чтобы она удовлетворяла условию Коши.

Непрерывность функции многих переменных.

1-е определение. Функция многих переменных f(M) называется непрерывной в т.M₀, если предельное значение этой функции в т. M₀ существует и оно равно частному значению f(M₀) этой функции в т.M₀ =f(M₀).

2-е определение. Функция многих переменных f(M) называется непрерывной в т. M₀, если для любого έ>0 найдется число б>0 такое, что при выполнении условия ρ(M₀,M)<б удовлетворяется неравенство |f(M)-f(M₀)|<έ.

Приращение функции многих переменных.

Полным приращением ∆U функции U=f(M) в точке M₀ называется разность f(M)-f(M₀), т.е. ∆U=f(M)-f(M₀)=f(x₁x₂,…,x_n)-f(x₁₀,x₂₀,…,x_n0)

Частным приращением ∆U функции многих переменных f(M) в т. M₀ по переменной x_i называется разность ∆x_iU=f(x₁₀,x₂₀,…,x_io+∆x_i,…,x_m0)-f(x₁₀,x₂₀,…,x_i0,…,x_m0).

Частные производные и дифференцируемость: Если существует конечное предельное значение отношения при ∆x_m->0 (в т. M₀), то это значение называется частной производной функции f(M) в т. M₀ и обозначается: , т.е. .

При вычислении частной производной по переменной x_i все остальные переменные считаются фиксированными.

Функция U=f(x₁,x₂,…,x_m) называется дифференцируемой в т. M(x₁,x₂,…,x_m), если полное ее приращение в т. M представимо в виде ∆U=A₁∆x₁+A₂∆x₂+…+A_m∆x_m+o(∆x₁)+o(∆x₂)+…+o(∆x_m), где A₁,A₂,…,A­_m-некоторые числа независящие от ∆x_i (i=1,2,…,m).

Теорема 18. Пусть функция U=f(x₁,x₂,…,x_m) дифференцируема в т. M(x₁,x₂,…,x_m), тогда она имеет частные производные по всем переменным. При этом выполняется равенство A₁= , A₂= ,…, A_m= .

Доказательство. По условию теоремы функция U=f(x₁,x₂,…,x_m) дифференцируема в т. M. Следовательно для ее приращения ∆U можно записать : ∆U=A₁∆x₁+A₂∆x₂+…+A_m∆x_m+o(∆x₁)+o(∆x₂)+…+o(∆x_m). Зафиксируем все координаты, кроме x_i тогда ∆x_iU=A_i∆x_i+o(∆x_i). Посмотрим существует ли частная производная определению Т.о. A_i= (i=1,2,…,m).

Дифференциал: Определение: Дифференциалом dU дифференцируемой функции U=f(x₁,x₂,…,x_m) в точке M называется главная линейная часть приращения dU= A₁∆x₁+A₂∆x₂+…+A_m∆x_m= + .

Теорема 19. Пусть функция U=f(x₁,x₂,…,x_m) дифференцируема в точке M(x₁,x₂,…,x_m). Пусть кроме того, функции x₁= ₁(t₁,t₂,…,t_k), x₂= ₂(t₁,t₂,…,t_k),…, x_m= _m(t₁,t₂,…,t_k) дифференцируемы в т. N(t₁,t₂,…,t_k). Тогда сложная U( ₁(t₁,t₂,…,t_k),…, _m(t₁,t₂,…,t_k)) дифференцируема в т. N. При том справедливы следующие равенства:

;

; … ;

.

Доказательство: Т.к. функция U=f(x₁,x₂,…,x_m) дифференцируема в точке M, то справедливо равенство:

В свою очередь функции дифференцируемы в т. N , соответствующей т. M, т.е. для них справедливы равенства ∆x_i= + . I=(1,2,…,m).

+ + ( + + +

Частные производные и дифференциалы высших порядков. Если функция U=f(x₁,x₂,…,x_m) дифференцируема, то существуют частные производные (i=1,2,…,m) Производная есть функция многих переменных =g(x₁,x₂,…,x_m). Далее, если функция g(x₁,x₂,…,x_m) дифференцируема в т.M, то существуют производные: (k=1,2,…,m)= - вторая производная функции U по переменной x_i,x_k. Вторая производная функции U=f(x₁,x₂,…,x_m) обозначается символами: . Если i≠k, то вторая производная называется смешанной производной.

Локальный экстремум функции многих переменных. Функция U=f(x₁,x₂,…,x_m) имеет в т. M₀ локальный минимум (локальный максимум), если найдется δ-окрестность т. M₀, в пределах которой значение функции f(M) является наименьшим(наибольшим). Вместе локальный минимум и локальный максимум называются локальным экстремумом.

Теорема 21. Пусть функция U=f(x₁,x₂,…,x_m) имеет производную 1-го порядка по всем переменным в т. M₀ и т. M₀ является точкой локального экстремума. Тогда все производные 1-го порядка этой функции равны 0 в т. M₀ , т.е.

Доказательство. Выберем произвольную переменную x_i. Зафиксируем все переменные, кроме x_i. Тогда функция U=f(M) станет функцией одной переменной U=f(x₁₀,..,x_i,…,x_m0), будет иметь экстремум в т. М₀. Но для функции одной переменной необходимым условием экстремума является равенство ,2,..,m)По-другому необходимое условие экстремума можно записать dU|M₀=0.

Критерий Сильвестра: Для того чтобы кв. форма была положительно определенной необходимо и достаточно, чтобы все главные миноры матрицы кв. формы были положительны. Для того чтобы кв. форма была отрицательно определенной необходимо и достаточно, чтобы знаки главных миноров матрицы кв. формы чередовались, при том А₁<0.

ТЕОРЕМА 22: Пусть ф-ция U=f( ….. ) один раз дифференцируема в точке и некоторой ее окрестности. Пусть кроме того точка является точкой возможного экстремума (т.е =0).

Тогда если 2ой дифференциал является положительным (отрицательным) определенной квадратной формой , то ф-ция U=f( ….. ) достигает в точке локального min(max); если же квадратичная форма является знакопеременной ,то экстремума в точке нет. (без д.)

Схема исследования ф-ций многих переменных на экстремум:

1. Использование необходимости условия (i=1…m) находим точки возможного экстр.

2. Каждую из этих точек исследуем на знакоопределенность 2ой дифференциал (i=1…m); Возможны 2 случая:

А) >0….. >0 = то в точке -min

Б) если <0; >0; <0 ….. то в точке -max

В) Для ф-ции двух переменных U=f(x,y), если <0 то в точке экстремума нет.

Условный экстремум: это экстремум ф-ции при условии, что на переменной ф-ции положены некоторые дополнительные связи.

Метод Лагранжа:Ψ=f+ +….+ , где 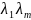-неопределенный. Необходимые условия экстремума в этом случае есть. = 1+…+ n+ 1+…+ m=0. Можно выбрать коэф. ,таким образом, чтобы выполнялось равенство: ; =0

Действительно ,исходя из этих равенств и опр. Ψ можно получить

Если определитель этой системы не равен 0 , то имеется единственное решение этой системы. Если условия …. выполняется то в остаются только независимые переменные. Это означает что условие будет выполняться при выполнении равенств ..

В итоге для определения X1..Xn,Y1..Ym и -получается n+2m ур-ний.

Достаточное условие в этой задаче надо использовать в виде >0-min <0-max.

Дифференцирование ф-ции заданной неявно:Пусть ф-ция многих переменных U=f( ….. ) задана неявно равенством F( ….. ,U)=0 F-дифференциал в окрестности некоторой точки. Производная от сложной ф-ции переменной , равна (i=1…m)

Уравнение касательной плоскости: Опр: касательной плоскостью к поверхности Z=f(x,y) в точке No(Xo,Yo,Zo) называется плоскость , для которой угол между плоскостью и произвольной секущей, проходящий через точки стремиться к 0 при N1->N0 Уравнение касательной:

P: (X-Xo)+ (Y-Yo)-(Z-Zo)=0

Производная по направлению, градиент: Опр: Производная ф-ции U по переменной при (т.е в точке Mo) называется производной ф-ции по направлению в точке Mo(Xo,Yo,Zo) и обозначается

Опр: Градиентом ф-ции f(x,y,z) в произвольной точке М называется вектор с координатами , , grad U={ , , = + j + k

Инвариантность формы 1го дифференциала: Рассмотрим ф-цию многих переменных U=f( ….. ) пусть она дифференцируема в точке Mo( ….. ) выражение для 1го диф-ла этой ф-ции имеет вид: +…+ это выражение записано при условии что переменные ….. являются независимыми.

Теорема 23(Формула тейлора для ф-ции многих переменных): Пусть ф-ция U=f( ….. ) определена на некоторой ξ окрестности точки Mo( ….. ) и (n+1) раз диф. в этой же окрестности. Тогда полное приращение ф-ции ∆U=f(M)-f(Mo) в точке Мо можно представить в виде: ∆U=f(M)-f(Mo)= U + ;где No некоторая точка из ξ окрестности точки Мо

Числовые ряды: Опр ряда: Выражение называется числовым рядом. эл-ты ряда.

Опр: Частичной суммой Sn ряда называется сумма первых n элементов этого ряда Sn=

Опр: Ряд называется сходящимся если сходится последовательность {Sn} его частичной суммы, т.е если сущ. =S в это случае S называют суммой ряда и правомерна запись =S . Если же . не существует то ряд наз. расходящимся.

Теорема 24(критерий Коши):Для того что бы ряд сходился необходимо и достаточно, что бы для любого ξ>0 нашлось число N такое, что при n>=N и при любых натуральных P выполнялось неравенство: >ξ

Док-во: из критерия коши для последовательности {Sn} при n>=N и любых натуральных Р должно выполнятся <ξ. По определению Sn+p= =U1+..Un+Un+1+..+Un+p; Sn= = (вычтем) Sn+p-Sn=Un+1+..+Un+p= Следовательно при n>=N и любом Р <ξ

Необходимый признак сходимости числового ряда: используем критерий Коши для Р=1 тогда = <ξ при n>=N Последнее опр. Б.м последовательности: т.е для сходимости ряда необходимо выполнение равенства =0

Числовые ряды с неотрицательными элементами: Числовые ряды -с неотриц. эл-ми (т.е Р>=0) принято называть рядами с положительными эл-ти. Из опр. следует, что последовательность {Sn} частичных сумм этого ряда является неубывающей.

Теорема 25: Для того что бы ряд с положительными эл-ми сходился необходимо и достаточно, чтобы последовательность {Sn} его частичных сумм была ограниченна.

Теорема 26: (общий признак сравнения) Пусть и два ряда с положительными эл-ми и пусть для всех номеров выполняется неравенство Pk<=Pk’(Pk>=Pk’) тогда из сходимости (расходимости) ряда следует сходимость(расходимость) ряда

Док-во: (Pk<=Pk’) Если это так, то выполняется неравентсво Sn<=Sn’ по условию теоремы сходится следовательно последовательность {Sn’} сходится и является ограниченной т.е и последовательность {Sn} для которой справедливо неравенство Sn<=Sn’ так же является ограниченной и сходящейся. Замечание: В формулировке теоремы можно заметить условие выполнения неравенства Pk<=Pk’ для всех k по условию выполнения неравенства Pk<=Pk’ начиная с некоторого номера.

Теорема 27: и -два ряда со строго положительными эл-ми(Pk>0 Pk’>0) и пусть для всех номеров K выполняется неравенство ( ) , тогда из сходимости (расходимости) ряда следует сходимость (расходимость)

Док-во: Пусть выполняется ; запишем это нер-во для k=1,2..(n-1)

… перемножим нер-ва и получим: ; Pn=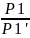 *Pn’=cPn’(c= )

Следовательно если ряд выбрать ряд геометрической прогрессии (такой ряд сходится при q<1 и расходится при q=1) то из общего признака сравнения можно получить два признака Даламбера и Коши.

Признак Даламбера (Т28):Пусть для всех k верно неравенство ( ), тогда ряд сходится (расходится)

Док-во: Возьмем в качестве ряда сравнение ряд геометрической прогрессии . Тогда

и и подставим эти выражения в исходные неравенства. Получим: тогда, в соответствии с предыдущей теоремой 27, ряд сходится(расходится), если сходится(расходится) ряд

Признак Даламбера (Т29): Пусть существует предел =l , тогда ряд сходится, если l<1, и расходится если l>1 . При l=1 признак не работает.

Признак Коши(Т30):Пусть для всех номеров k (или начиная с номера ) выполняются неравенства: 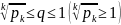.Тогда ряд сходится (расходится)

Док-во: В качестве ряда сравнения вновь выберем ряд геометрической прогрессии:

. Возведем в k-ю степень исходное неравенство. Получим: ,

В соответствии с общим признаком сравнения из сходимости(расходимости) ряда

следует сходимость(расходимость) ряда

Признак Коши(Т31): Пусть существует предел . Тогда ряд сходится, если l>1 признак не работает.

Теорема 32:Пусть функция f(x) не определена и не возрастает при (m-некоторое натуральное число), тогда ряд сходится в том и только в том случае, когда существует предел последовательности { }, где = , т.е. существует .

Признак сравнения в терминах порядков величин Пусть при элемент ряда порядок т.е при . Тогда при ряд сходится и при расходится

Знакопеременный ряд: Знакочередующимся рядом называется ряд , где

Абсолютная и условная сходимость: Опр: Ряд называется абсолютно сходящимся если, сходится ряд Опр: Если ряд не сходится, и сходится, то он называется условно сходящимся.

Теорема33 (о сходимости абсолютно сходящегося ряда): Пусть ряд сходится. Тогда и ряд так же сходится.

Теорема 34 (Признак Лейбица): Пусть последовательность модулей знакочередующегося ряда является не возрастающей и бесконечно малой, т.е. (k=1,2,…) , тогда ряд является сходящимся.

Док-во: Частичную сумму составленную из четного кол-ва элементов, т.е. Представим это выражение в виде: следовательно последовательность явл. неубывающей.

Представим теперь в другом виде: , < т.е. послед - являтся ограниченной сверху.

Теорема 35 (Признак Дирихле-Абеле): Пусть для ряда выполняются два условия:

1.Последовательность является невозрастающей и бесконечно малой.

2.Последовательнность частичных сумм ряда является ограниченной.

Тогда ряд сходится.

Функциональные последовательности и ряды(определения, область сходимости, сходимость и равномерная сходимость). Определение: Функциональной последовательностью {f_n(x)} называется мн-во функций f₁(x),f₂(x),…,f_n(x),…, заданных на мн-ве {x}. Определение: Мн-во {x} точек сходимости последовательности {f_n(x)} называются областью сходимости этой посл-ти. На этом мн-ве посл-ть {f_n(x)} сходится к некоторой ф-ии f(x), т.е. . Определение: Функциональная посл-ть {f_n(x)} называется сходящейся к ф-ии f(x) на мн-ве {x}, если для любого ε>0 и каждого найдется число такое, что при выполняется неравенство: Определение: Функциональная последовательность {f_n(x)} называется равномерно сходящейся к ф-ии f(x) на множестве {x}, если для любого ε>0 найдется число такое, что при и сразу для всех выполняется неравенство: . Определение: Выражение вида называется функциональным рядом. Определение: Мн-во {x} точек сходимости функционального ряда называются его областью сходимости. Определение: Функциональный ряд называется сходящимся на мн-ве {x}, если соответствующая посл-ть частичных сумм {S_n(x)} является сходящейся на мн-ве {x}. Определение: Функциональный ряд является равномерно сходящимся на мн-ве {x}, если соответствующая посл-ть частичных сумм {S_n(x)} является равномерно сходящейся на мн-ве {x}.

Теорема 37 (Критерий Коши для функциональных последовательностей): Для того чтобы функциональная последовательность {f_n(x)} сходилась равномерно к ф-ии f(x) на множестве {x}, необходимо и достаточно, чтобы для любого ε>0 нашлось число такое, что при , для всех натуральных р и сразу для всех выполнялось неравенство: .

Теорема 38 (Критерий Коши для функциональных рядов): Для того чтобы функциональный ряд сходилась равномерно к сумме S(x) на множестве {x}, необходимо и достаточно, чтобы для любого ε>0 нашлось число такое, что при , для всех натуральных р и сразу для всех выполнялось неравенство: .

Теорема 39 (Признак Вейерштрасса): Пусть функциональный ряд задан на мн-ве {x} и пусть существует сходящийся числовой ряд , такой, что для всех k и всех выполняется неравенство: , тогда функциональный ряд сходится равномерно на множестве {x}.

Теорема 40 (Непрерывность): Пусть функциональный ряд равномерно сходится к сумме S(x) на мн-ве [a,b] и пусть элементы этого ряда непрерывны на [a,b], тогда и сумма S(x) ряда непрерывна на [a,b].

Теорема 41 (почленное интегрирование): Пусть функциональный ряд равномерно сходится к сумме S(x) на мн-ве [a,b] и пусть элементы этого ряда интегрируемы на [a,b], тогда и сумма S(x) ряда интегрируема на [a,b], и справедлива формула почленного интегрирования:

.

Теорема 42 (почленное дифференцирование): Пусть элементы функционального ряда дифференцируемы на [a,b] и ряд из производных равномерно сходится на [a,b]. Пусть кроме того сам ряд сходится хотя бы в 1 точке . Тогда ряд сходится равномерно к сумме S(x) на [a,b] и справедлива формула почленного дифференцирования:

.

Степенные ряды: Определение: Функциональный ряд вида (или в более общем случае ) называется степенным рядом.

Теорема 43 (Коши-Адамара): Состоит из 3-х утверждений:

1. Пусть последовательность не ограничена. Тогда ряд имеет единственную точку сходимости х=0.

2. Пусть последовательность ограничена и её верхний предел . Тогда ряд сходится абсолютно при и расходится при .

3. Пусть последовательность ограничена и её верхний предел . Тогда ряд сходится абсолютно на всей числовой оси.

Теорема 44 (Радиус сходимости числового ряда): Для любого степенного ряда существует положительное число R такое, что при ряд сходится абсолютно, а при ряд расходится. Число R называется радиусом сходимости степенного ряда, и вычисляется по формуле: .

Теорема 45 (Непрерывность степенного ряда): Сумма S(x) степенного ряда является непрерывной функцией на интервале сходимости (-R,R).

Теорема 46 (почленное интегрирование степенного ряда): Степенной ряд можно почленно интегрировать на любом сегменте [0,x], где

Теорема 47 (почленное дифференцирование степенного ряда): Степенной ряд можно почленно дифференцировать на интервале (-R,R).

Разложение функции в степенной ряд: Определение: Функция f(x) может быть разложена в степенной ряд на интервале (-R,R), если существует степенной ряд, который сходится к функции f(x) на (-R,R).

Ряд Тейлора: Определение: Степенной ряд , коэффициенты которого вычисляются по формуле называются рядом Тейлора для функции f(x). Т.е. ряд Тейлора для ф-ии f(x) имеет вид:

.