
- •3. Экстремумы функции. Исследование функции на экстремум с помощью первой производной.
- •4. Наибольшее и наименьшее значение функции на отрезке.
- •5. Асимптоты. Схема построения графика функции
- •6.Первообразная. Неопределенный интеграл, его свойства
- •7. Основные табличные интегралы
- •Неопределенный интеграл степенной функции
- •Неопределенный интеграл експоненты показательной функции
- •8. Интегрирование способом подстановки
- •9.Определеный интеграл.Геометрический смысл
- •10. Вычисление площадей плоских фигур через определенный интеграл
- •12.Деление отрезка в данном отношении.
- •Операции над векторами в прямоугольной системе координат.
- •13. Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
- •14.Уравнение прямой в отрезках.
- •15.Взаимное расположения прямых.
- •16.Угол между прямыми
- •17.Аксиомы стереометрии
- •18.Признак параллельности двух плоскостей
- •20.Перпендикуляр и наклонные к плоскости. Теорема о трех перпендикулярах
- •21.Двугранный угол. Признак перпендикулярности двух плоскостей
- •22.Призмы. Виды призм. Площадь поверхности
- •23.Параллелепипед. Виды и свойства
- •25.Площадь поверхности пирамиды
- •26.Усеченная пирамида. Площадь ее поверхности
- •31.Конус. Усеченный конус. Площадь поверхности конуса и усеченного конуса
- •36.Кривые второго порядка
1.Вторая
производная функции. Геометрический
и физический смысл производной.
Произво́дная (функции
в точке) — основное понятие дифференциального
исчисления,
характеризующее скорость изменения
функции (в данной точке). Определяется
как предел отношения
приращения функции к приращению
ее аргумента при
стремлении приращения аргумента к нулю,
если такой предел существует. Функцию,
имеющую конечную производную (в некоторой
точке), называют дифференцируемой (в
данной точке). Процесс вычисления
производной называется дифференци́рованием.
Обратный процесс — интегрирование
Производной
функции
f(x) (f'(x0))
в точке x0 называется
число, к которому стремится разностное
отношение


![]() ,
стремящемся к нулю.
,
стремящемся к нулю.![]()

2.Признаки
возрастания и убывания функций.
Одна из основных задач исследования
функции — это нахождение промежутков
ее возрастания и убывания. Такое
исследование легко провести с помощью
производной. Сформулируем соответствующие
утверждения.
Достаточный
признак возрастания функции. Если
f’(х) > 0 в каждой точке интервала I, то
функция f возрастает на I.
Достаточный
признак убывания функции. Если
f’(х) < 0 в каждой точке интервала I, то
функция f убывает на I.
Доказательство
этих признаков проводится на основании
формулы Лагранжа (см. п. 19). Возьмем два
любых числа х1 и
x2 из
интервала. Пусть x1<x2.
По формуле
Лагранжа существует
число с∈(х1,
x2),
такое, что Число с принадлежит интервалу
I, так как точки х1 и
x2 принадлежат
I. Если f'(x)>0 для х∈I
то
f’(с)>0,
и
поэтому
F(x1)<F(x2)
— это следует из формулы (1), так как
x2 —
x1>0.
Этим доказано возрастание функции f на
I. Если же f’ (x)<0 для х∈I
то
f'(с)<0,
и
потому
f(x1)>f
(х2)
— следует из формулы (1), так как x2—x1>0.
Доказано убывание функции f на I. Наглядный
смысл признаков ясен из физических
рассуждений (рассмотрим для определенности
признак возрастания).
Пусть
движущаяся по оси ординат точка в момент
времени t имеет ординату y = f(t). Тогда
скорость этой точки в момент времени
t равна f'(t) (см. Мгновенная
скорость).
Если f’ (t)>0 в каждый момент времени
из промежутка t, то точка движется в
положительном направлении оси ординат,
т. е. если t1 <t2,
то f (t1)<f
(t2).
Это означает, что функция f возрастает
на промежутке I.
![]()
3. Экстремумы функции. Исследование функции на экстремум с помощью первой производной.
Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x1< x2 выполняется неравенство (f(x1) < f(x2) (f(x1) > f(x2)).
Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f '(x) 0
(f ' (x) 0).Точка xо называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки xо, для всех точек которой верно неравенство f(x) ≤ f(xо) (f(x) ≥ f(xо)).
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.
Если в некоторой окрестности точки х0 выполняется неравенство f(x)<f(х0) или f(x) > f(х0), то точка х0 называется точкой экстремума функции f(x) (соответственно точкой максимума или минимума). Необходимое условие экстремума: если х0 – экстремальная точка функции f(x), то первая производная f’(х0) либо равна нулю или бесконечности, либо не существует. Достаточное условие экстремума: х0 является экстремальной точкой функции f(x), если ее первая производная f’(x) меняет знак при переходе через точку х0: с плюса на минус – при максимуме, с минуса на плюс – при минимуме.Точка х0 называется точкой перегиба кривой y=f(х),если при переходе через точку х0 меняется направление выпуклости. Необходимое условие точки перегиба: если х0 – точка перегиба кривой y=f(х), то вторая производная f’’(х0) либо равна нулю или бесконечности, либо не существует. Достаточное условие точки перегиба: х0 является точкой перегиба кривой y=f(х), если при переходе через точку х0 вторая производная f’’(х) меняет знак.
Прямая yас=kх+b называется наклонной асимптотой кривой y=f(х), если расстояние от точки (x; f(х)) кривой до этой прямой стремится к нулю при х . При этом
![]()
![]()
При k=0 имеем горизонтальную асимптоту:y=b.
Если
![]()
то прямая х=а называется вертикальной асимптотой
4. Наибольшее и наименьшее значение функции на отрезке.
Чтобы найти наибольшее или наименьшее значение функции на отрезке, нужно исследовать поведение функции на данном отрезке с помощью производной.
Для
этого мы
следуем известному алгоритму:1.
Находим ОДЗ функции.2.
Находим производную функции3.
Приравниваем производную к нулю4.
Находим промежутки, на которых производная
сохраняет знак, и по ним определяем
промежутки возрастания и убывания
функции:Если на промежутке I производная
функции ![]() ,
то функция
,
то функция ![]() возрастает
на этом промежутке.Если
на промежутке I производная функции
возрастает
на этом промежутке.Если
на промежутке I производная функции ![]()
![]() ,
то функция
убывает
на этом промежутке.5.
Находим точки
максимума и минимума функции.В точке
максимума функции производная меняет
знак с «+» на «-».В точке
минимума функции производная меняет
знак с «-» на «+».6.
Находим значение функции в концах
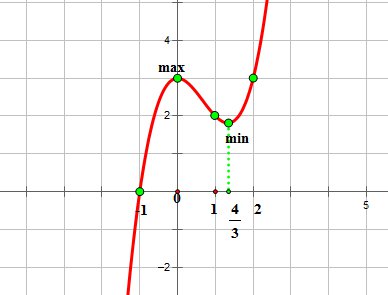
отрезка,Рассмотрим функцию
,
то функция
убывает
на этом промежутке.5.
Находим точки
максимума и минимума функции.В точке
максимума функции производная меняет
знак с «+» на «-».В точке
минимума функции производная меняет
знак с «-» на «+».6.
Находим значение функции в концах
отрезка,Рассмотрим функцию ![]() .
График этой функции выглядит так:
.
График этой функции выглядит так:
5. Асимптоты. Схема построения графика функции
Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.
Определение 7.1 Вертикальной
асимптотой графика
функции ![]() называется
вертикальная прямая
называется
вертикальная прямая ![]() ,
если
,
если ![]() или
или ![]() при
каком-либо из условий:
при
каком-либо из условий: ![]() ,
, ![]() ,
, ![]() .
Заметим, что мы при этом не требуем,
чтобы точка
.
Заметим, что мы при этом не требуем,
чтобы точка ![]() принадлежала
области определения функции
принадлежала
области определения функции ![]() ,
однако она должна быть определена по
крайней мере в какой-либо из односторонних
окрестностей этой точки:
,
однако она должна быть определена по
крайней мере в какой-либо из односторонних
окрестностей этой точки: ![]() или
или ![]() ,
где
,
где ![]() .
.
Пример 7.1
Рассмотрим функцию 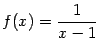 .
График
имеет
вертикальную асимптоту
.
График
имеет
вертикальную асимптоту ![]() ,
поскольку при
,
поскольку при ![]() выполняется
условие
выполняется
условие ![]() ,
а также при
,
а также при ![]() выполняется
условие
выполняется
условие ![]() .
.

