
Свойства
Арифметические свойства
Если
и
![]() аналитичны
в области
аналитичны
в области
![]()
Функции
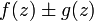 ,
,
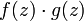 и
и
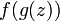 аналитичны
в
аналитичны
в
 .
.Если в области не обращается в ноль, то
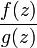 будет
аналитична в
будет
аналитична в
Если
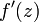 в
области
не
обращается в ноль, то
в
области
не
обращается в ноль, то
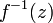 будет
аналитична в
будет
аналитична в
Аналитическая функция бесконечно дифференцируема в своей области аналитичности. Обратное в общем случае неверно.
Некоторые свойства аналитических функций близки к свойствам многочленов, что, впрочем, и неудивительно — определение аналитичности в смысле Вейерштрасса свидетельствует о том, что аналитические функции — в некотором роде предельные варианты многочленов. Допустим, согласно основной теореме алгебры любой многочлен может иметь нулей числом не более его степени. Для аналитических функций справедливо аналогичное утверждение, вытекающее из теоремы единственности в альтернативной форме:
Если множество нулей аналитической в односвязной области функции имеет в этой области предельную точку, то функция тождественно равна нулю.
Интегральная теорема Коши
Теорема
Для
любой функции
,
аналитической
в некоторой односвязной
области
![]() и
для любой замкнутой кривой
справедливо
соотношение
и
для любой замкнутой кривой
справедливо
соотношение
![]()
Доказательство
Из
условия аналитичности
(уравнений Коши—Римана) следует, что
дифференциальная
форма
![]() замкнута.
Пусть теперь
замкнута.
Пусть теперь
![]() —
замкнутый самонепересекающийся
кусочно-гладкий контур внутри области
определения функции
,
ограничивающий область
.
Тогда по теореме
Стокса
имеем:
—
замкнутый самонепересекающийся
кусочно-гладкий контур внутри области
определения функции
,
ограничивающий область
.
Тогда по теореме
Стокса
имеем:
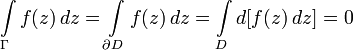
Формула Коши
Пусть
функция
![]() аналитическая
в односвязной замкнутой области
аналитическая
в односвязной замкнутой области
![]() (
(![]() ),
с кусочно-гладкой границей
),
с кусочно-гладкой границей
![]() ,
ориентированной в положительном
направлении (рис. 142), т. е. против часовой
стрелки. Тогда имеет место формула Коши
,
ориентированной в положительном
направлении (рис. 142), т. е. против часовой
стрелки. Тогда имеет место формула Коши
![]() ,
,
где
![]() -
любая точка внутри контура
.
-
любая точка внутри контура
.
Таким
образом, аналитическую функцию достаточно
определить на контуре
,
а по формуле (1) можно автоматически
получить ее значения в других точках
![]() .
.
Для доказательства формулы (1) рассмотрим функцию
![]() .
(2)
.
(2)
Опишем
около точки
окружность
![]() (см.
рис. 142), ориентированную положительно,
достаточно малого радиуса
(см.
рис. 142), ориентированную положительно,
достаточно малого радиуса
![]() .
Функция
.
Функция
![]() определена
и непрерывна на
за
исключением точки
,
в которой ее предел равен производной
от
определена
и непрерывна на
за
исключением точки
,
в которой ее предел равен производной
от
![]() в
:
в
:
![]() .
.
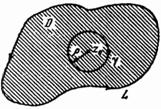
Рис. 142
Поэтому,
если доопределить функцию
![]() в
при
помощи равенства
в
при
помощи равенства
![]() ,
то она окажется определенной, непрерывной
и ограниченной на
:
,
то она окажется определенной, непрерывной
и ограниченной на
:
![]() ,
,
![]() .
.
К
тому же функция
аналитична
на множестве, ограниченном контурами
![]() и
и
по теореме 3 § 6.6
и
и
по теореме 3 § 6.6
 .
.
Но
правая часть этого равенства стремится
при
![]() к
нулю:
к
нулю:
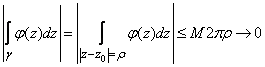 ,
,
а левая не зависит от . Поэтому
![]()
Так как (см. (10) § 6.6)
![]() ,
,
формула Коши доказана.
Формула Коши имеет место и для многосвязной области и доказательство ее может быть сведено к уже доказанной формуле Коши для односвязной области.
На
рис. 143 изображена двусвязная область
с
положительно ориентированной границей
,
состоящей из двух замкнутых соответственно
ориентированных контуров
![]() .
.
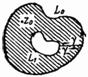
Рис. 143
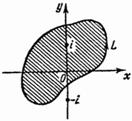
Рис. 144
Пусть
-
произвольная точка
.
Соединим контуры
![]() и
и
![]() кусочно-гладкой
кривой
,
ориентированной от
и
,
не проходящей через точку
.
Наряду с кривой
вводим
совпадающую с ней кривую
кусочно-гладкой
кривой
,
ориентированной от
и
,
не проходящей через точку
.
Наряду с кривой
вводим
совпадающую с ней кривую
![]() ,
но ориентированную противоположно.
,
но ориентированную противоположно.
Если
из
выкинуть
,
то оставшаяся область
![]() будет
односвязной с положительно ориентированной
границей:
будет
односвязной с положительно ориентированной
границей:
![]() .
.
Функция
аналитическая,
на
![]() и
и
![]() .
Поэтому на основании теоремы Коши для
односвязной области
.
Поэтому на основании теоремы Коши для
односвязной области
![]()
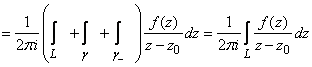 ,
,
потому
что
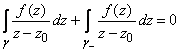 .
.
Пример. Вычислить интеграл
![]() ,
,
где
-
ориентированный против часовой стрелки
контур, содержащий в себе точку
![]() (рис.
144) и такой, что точка
(рис.
144) и такой, что точка
![]() находится
вне него. Запишем наш интеграл в виде
находится
вне него. Запишем наш интеграл в виде
![]()
и
рассмотрим функцию
![]() .
В силу наших предположений о контуре
эта
функция аналитична в замкнутой области,
ограниченной контуром
,
поэтому по формуле Коши
.
В силу наших предположений о контуре
эта
функция аналитична в замкнутой области,
ограниченной контуром
,
поэтому по формуле Коши
![]() .
.
Изолированная особая точка — точка, в некоторой проколотой окрестности которой функция однозначна и аналитична, а в самой точке либо не задана, либо не дифференцируема.
