
Геометрическая интерпретация комплексного числа
Всякое комплексное число z = (x, y) можно изобразить как точку на плоскости с координатами x и y. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy - мнимой.
Расстояние r точки z от нулевой точки, т. е. число
![]()
![]()
называется модулем комплексного числа z и обозначается символом |z|.
Число
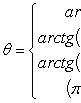
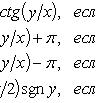
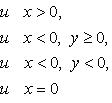
называем
аргументом
комплексного числа z
и обозначаем символом θ
= arg z.
При заданном r
углы, отличающиеся на
![]()
![]() ,
соответствуют одному и тому же числу.
В этом случае записываем
,
соответствуют одному и тому же числу.
В этом случае записываем
![]()
![]()
![]() называем
главным
значением
аргумента.
называем
главным
значением
аргумента.
Числа r и θ называют полярными координатами комплексного числа z. В этом случае
z = (x, y) = (r cos θ, r sin θ) = r(cos θ + i sin θ)
называется тригонометрической формой комплексного числа.
Если z1 = (r1 cos θ1, r1 sin θ1), z2 = (r2 cos θ2, r2 sin θ2), то
z1z2 = (r1r2 cos(θ1 + θ2), r1r2 sin(θ1 + θ2)),
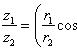
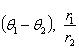
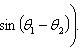
Для n-й степени числа z = (r cos θ, r sin θ) формула приобретает вид zn = (rn cos nθ, rn sin nθ).
При r = 1 соотношение приобретает вид zn = (cos nθ, sin nθ) и называется формулой Муавра.
Корень n-й степени из комплексного числа z имеет n различных значений, которые находятся по формуле
![]()
![]()
![]()
![]()
![]() (1)
(1)
Неравенство Бесселя
Рассмотрим кусочно непрерывную функцию f (x), заданную в интервале [−π, π]. Ее разложение в ряд Фурье имеет вид
![]()
В неравенстве Бесселя устанавливается, что
![]()
Отсюда
следует, что ряд
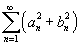 сходится.
сходится.
Равенство Парсеваля
Если f (x) является квадратично интегрируемой функцией в интервале [−π, π], так что выполняется соотношение
![]()
то неравенство Бесселя становится равенством. В этом случае справедлива формула Парсеваля:
![]()
Формула Парсеваля в комплексной форме
Снова предположим, что f (x) является квадратично интегрируемой функцией в интервале [−π, π]. Пусть cn − ее комплексные коэффициенты Фурье, то есть
![]()
где
![]()
Тогда формула Парсеваля записывается в виде
![]()
Заметим, что энергия 2π-периодической волны f (x) равна
![]()
Определение ряда Фурье
Говорят, что функция f (x) имеет период P, если f (x + P) = f (x) для всех значений x. Пусть период функции f (x) равен 2π. В этом случае достаточно рассмотреть поведение функции в интервале [−π, π].
Предположим, что функция f (x) с периодом 2π абсолютно интегрируема в интервале [−π, π]. При этом является конечным так называемый интеграл Дирихле:
![]()
Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).
Если условия 1 и 2 выполнены, то ряд Фурье для функции f (x) существует и сходится к данной функции (Смотрите об условиях сходимости также раздел Сходимость рядов Фурье). Если x0 − точка разрыва, то ряд Фурье сходится к значению
![]()
Ряд Фурье функции f (x) представляется в виде
![]()
где коэффициенты Фурье a0, an и bn определяются формулами
![]()
Иногда используются альтернативные формы записи для разложения в ряд Фурье. Заменяя an и bn новыми переменными dn и φn или dn и θn , где
![]()
можно, соответственно, записать
![]()
Разложение в ряд Фурье четных и нечетных функций
Разложение в ряд Фурье четной функции f (x) с периодом 2π не содержит синусов и имеет вид
![]()
где коэффициенты Фурье определяются выражениями
![]()
Аналогично, разложение в ряд Фурье нечетной функции f (x), имеющей период 2π содержит только синусы и имеет вид
![]()
где ы bn равны
![]()
Ниже мы рассмотрим некоторые типичные примеры разложения функций с периодом 2π в ряд Фурье, предполагая, что такие разложения существуют и сходятся к заданной функции.
Четные и нечетные продолжения
Предположим, что f (x) является кусочно-непрерывной функцией, заданной в интервале [0, π]. Чтобы найти разложение данной функции в ряд Фурье, нужно продолжить ее и построить в интервале [−π, π]. Это можно сделать двумя способами:
можно построить четное продолжение f (x):
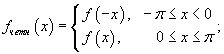
или построить нечетное продолжение f (x):

В случае четной функции разложение в ряд Фурье описывается выражением
![]()
где
![]()
В случае нечетной функции, соответственно, получаем
![]()
где коэффициенты разложения равны
![]()
Понятие четного и нечетного продолжения функции можно ввести и для непериодической функции. Пусть функция f (x) определена в интервале [0, L]. Используя четное продолжение данной функции на интервал [− L, L], получим следующую формулу разложения в ряд Фурье:
где
![]()
В случае нечетного продолжения соответствующая формула имеет вид
![]()
где коэффициенты bn равны
![]()
Ряды Тейлора и Маклорена
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
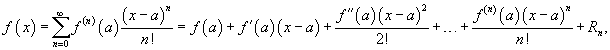
где Rn − остаточный член в форме Лагранжа определяется выражением
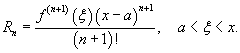
Если
приведенное разложение сходится в
некотором интервале x,
т.е.
![]() ,
то оно называется рядом
Тейлора,
представляющим разложение функции f
(x)
в точке a.
Если a
= 0, то такое
разложение называется рядом
Маклорена:
,
то оно называется рядом
Тейлора,
представляющим разложение функции f
(x)
в точке a.
Если a
= 0, то такое
разложение называется рядом
Маклорена:
![]()
Разложение некоторых функций в ряд Маклорена
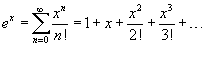
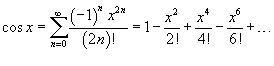
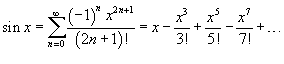
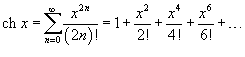
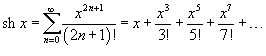
Биномиальный ряд
Знаменитая формула, изучаемая в школе под названием "бинома Ньютона", фактически была известна еще задолго до Ньютона. Ньютону же принадлежит заслуга ее распространения на случай не натуральных показателей.
Поставим вопрос о разложении функции
f(x) = (1 + x) μ
в ряд, расположенный по степеням x. Здесь
f '(x) = μ(1 + x) μ-1, f "(x) = μ(μ - 1)(1 + x) μ-2,
f ″′(x) = μ(μ - 1)(μ - 2)(1 + x) μ-3
и вообще
f (n)(x) = μ(μ - 1) ... (μ - n + 1)(1 + x) μ-n,
что можно подтвердить с помощью полной индукции.
Таким образом,
f(0) = 1, f '(0) = μ, f "(0) = μ(μ - 1), ...
..., f (n)(0) = μ(μ - 1) ... (μ - n + 1), ...
и ряд Тейлора нашей функции таков:
![]()
![]()
![]() (71)
(71)
Этот ряд называется биноминальным. Если μ = 0, 1, 2, то ряд (71) принимает соответственно вид
1, 1 + x, 1 + 2x + x2,
т. е. превращается в конечный многочлен. Нетрудно видеть, что это явление имеет место всегда, когда μ - целое неотрицательное число. Для таких значений μ равенство функции (1 + x) μ и суммы ее ряда Тейлора, т. е. равенство
![]()
![]()
![]()
![]()
![]()
справедливо при всех действительных (и даже комплексных!) x, что и составляет содержание элементарной теоремы о биноме Ньютона.
Если μ не есть целое неотрицательное число, то ряд (71) существенно бесконечен, и прежде всего встает вопрос о его промежутке сходимости.
Аналити́ческая функция (действительного переменного) — функция, которая совпадает со своим рядом Тейлора в окрестности любой точки области определения.
Однозначная
функция
![]() называется
аналитической
в точке
называется
аналитической
в точке
![]() ,
если сужение функции
на
некоторую окрестность
является
аналитической функцией. Если функция
аналитична в точке
,
то она аналитическая в каждой точке
некоторой окрестности точки
.
,
если сужение функции
на
некоторую окрестность
является
аналитической функцией. Если функция
аналитична в точке
,
то она аналитическая в каждой точке
некоторой окрестности точки
.
Аналитическая
функция (комплексного переменного) —
функция комплексного переменного
![]() (где
(где
![]() и
и
![]() —
вещественнозначные функции комплексного
переменного, являющиеся, соответственно,
вещественной и мнимой частью рассматриваемой
функции), для которой в каждой точке
некоторой области
—
вещественнозначные функции комплексного
переменного, являющиеся, соответственно,
вещественной и мнимой частью рассматриваемой
функции), для которой в каждой точке
некоторой области
![]() ,
называемой областью аналитичности,
выполняется одно из трёх равносильных
условий:
,
называемой областью аналитичности,
выполняется одно из трёх равносильных
условий:
Для вещественной и мнимой части этой функции в каждой точке
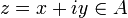 выполняются
условия
Коши — Римана
(аналитичность
в смысле Коши — Римана);
выполняются
условия
Коши — Римана
(аналитичность
в смысле Коши — Римана);Ряд Тейлора функции в каждой точке
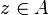 сходится
и его сумма равна
сходится
и его сумма равна
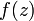 (аналитичность
в смысле Вейерштрасса);
(аналитичность
в смысле Вейерштрасса);Интеграл
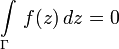 для
любой замкнутой кривой
для
любой замкнутой кривой
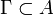 (аналитичность
в смысле Коши)
(аналитичность
в смысле Коши)
В курсе комплексного анализа доказывается эквивалентность трёх определений.
