
Теорема 1.2:
область сходимости степенного ряда (1.2) совпадает с одним из следующих интервалов:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ,
,
где
R –некоторое неотрицательное действительное
число или
![]() .
.
Число Rназываетсярадиусом сходимости,интервал – интервалом сходимостистепенного ряда (1.2).
Если
![]() ,то
интервал сходимости представляет собой
всю числовую ось
,то
интервал сходимости представляет собой
всю числовую ось
![]() .
.
Если
![]() ,то
интервал сходимости вырождается в точку
,то
интервал сходимости вырождается в точку
![]() .
.
Замечание:если
–
интервал сходимости для степенного
ряда (1.2), то
![]() –
интервал сходимости для степенного
ряда (1.1).
–
интервал сходимости для степенного
ряда (1.1).
Из
теоремы 1.2следует, что для практического
нахождения области сходимости степенного
ряда (1.2) достаточно найти его радиус
сходимостиR и выяснить вопрос о сходимости
этого ряда на концах интервала
сходимости
,т.
е. при
![]() и
и
![]() .
.
Теорема Абеля. Радиус и интервал сходимости
Теорема
Абеля. Пусть
степенной ряд
![]() сходится
в какой-то точке
сходится
в какой-то точке
![]() .
Тогда этот ряд сходится
.
Тогда этот ряд сходится
![]() (абсолютно).
(абсолютно).
Доказательство.
Ряд
сходится
в точке x1
в обычном смысле
![]() сходится
сходится
![]() числовая
последовательность
числовая
последовательность
![]() сходится
к нулю
сходится
к нулю
![]() ограничена,
то есть
ограничена,
то есть
![]()
Рассмотрим
.
Обозначим
![]()
Рассмотрим
![]() :
:
![]() сходится,
следовательно числовой ряд
(для
фиксированного x)
сходится по признаку сравнения
сходится
абсолютно на множестве | x
| < | x1
|
сходится,
следовательно числовой ряд
(для
фиксированного x)
сходится по признаку сравнения
сходится
абсолютно на множестве | x
| < | x1
|
Следствие.
Если степенной
ряд
расходится
в точке x2,
то этот ряд расходится
![]() .
.
Определение.
Если R -
неотричательное число или
![]() обладает
тем свойством, что степенной ряд
сходится
на множестве | x | < R и расходится на
множестве | x | > R, то R называется радиусом
сходимости данного степенного ряда. В
этом случае интервал ( − R,R) называется
интервалом сходимости степенного ряда.
Область сходимости степенного рядка
может не совпадать с интервалом
сходимости, так как может включаться
точка
обладает
тем свойством, что степенной ряд
сходится
на множестве | x | < R и расходится на
множестве | x | > R, то R называется радиусом
сходимости данного степенного ряда. В
этом случае интервал ( − R,R) называется
интервалом сходимости степенного ряда.
Область сходимости степенного рядка
может не совпадать с интервалом
сходимости, так как может включаться
точка
![]()
Теорема. У всякго степенного ряда есть радиус сходимости.
Доказательство. Пусть A - множество всех неотрицательных чисел, в которых степенной ряд сходится.
Так
как ряд сходится в точке
![]() (возможно
равная
).
Обозначим R
= supA.
Докажем, что R
- радиус сходимости степенного ряда.
(возможно
равная
).
Обозначим R
= supA.
Докажем, что R
- радиус сходимости степенного ряда.
Фиксируем
![]() по
определению точной верхней граним
по
определению точной верхней граним
![]() число
число
![]() так
как
так
как
![]() ряд
сходится в точке
ряд
сходится в точке
![]() по
теореме Абеля ряд сходится на множестве
| x
| < c,
в частности в точке x.
Так как x
- любая точка, такая что
по
теореме Абеля ряд сходится на множестве
| x
| < c,
в частности в точке x.
Так как x
- любая точка, такая что
![]() ряд
сходится на множестве | x
| < R.
ряд
сходится на множестве | x
| < R.
Фиксируем
![]() число
в | x
| > b
> R
такое что
число
в | x
| > b
> R
такое что
![]() .
То есть степенной ряд расходится в точке
.
То есть степенной ряд расходится в точке
![]() степенной
ряд расходится в точке x
(по следствию из теоремы Абеля)
ряд
расходится на множестве | x
| > R.
Следовательно R
= sup A
- радиус сходимости степенного ряда
.
степенной
ряд расходится в точке x
(по следствию из теоремы Абеля)
ряд
расходится на множестве | x
| > R.
Следовательно R
= sup A
- радиус сходимости степенного ряда
.
Лорана ряд, ряд вида
![]() ,
(*)
,
(*)
то есть ряд, расположенный как по положительным, так и по отрицательным степеням разности z — а (где z, а и коэффициенты ряда — комплексные числа). Совокупность членов с неотрицательными степенями представляет здесь обыкновенный степенной ряд, сходящийся, вообще говоря, внутри круга с центром а и радиусом R (£ ¥); остальные члены образуют ряд, сходящийся, вообще говоря, вне круга с тем же центром, но с радиусом r (r ³ 0). Если r < R, то ряд (*) сходится в круговом кольце r < |z — а| < R; его сумма является в этом кольце аналитической функцией комплексного переменного z.
Комплексным числом z называется пара (x, y) действительных чисел x и y. При этом равенство, сумма и произведение упорядоченных пар, а также отождествление некоторых из них с действительными числами определяются следующим образом:
1) два комплексных числа z1 = (x1, y1) и z2 = (x2, y2) называются равными, если x1 = x2 и y1 = y2;
2) суммой комплексных чисел z1 и z2 называется комплексное число z вида
z = (x1 + x2, y1 + y2);
3) произведением комплексных чисел z1 и z2 называется комплексное число
z = (x1x2 - y1y2, x1y2 + x2y1);
4)
множество комплексных чисел
![]()
![]() ,
отождествляется с множеством действительных
чисел R.
,
отождествляется с множеством действительных
чисел R.
Разностью комплексных чисел z1 и z2 называется комплексное число z такое, что z2 + z = z1, откуда находим z = z1 - z2 = (x1 - x2, y1 - y2).
Частным
комплексных чисел z1
и z2
называется комплексное число z
такое, что
![]() .
Отсюда находим
.
Отсюда находим
![]()
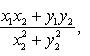
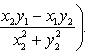
Комплексное
число (0, 1) обозначается символом i
= (0, 1). Тогда
![]()
![]() ,
т. е. i2
= -1. Произвольное комплексное число z
можно записать в виде
,
т. е. i2
= -1. Произвольное комплексное число z
можно записать в виде
z = (x, y) = (x, 0) + (0, y) = (x, 0) + (0, 1)(y, 0) = x + iy.
Эта
запись называется алгебраической
формой
комплексного числа. Комплексное число
![]()
![]() называется
сопряженным
по отношению к комплексному числу z
= (x,
y)
= x
+ iy.
называется
сопряженным
по отношению к комплексному числу z
= (x,
y)
= x
+ iy.
