
Функциональные последовательности
Определение.
Если каждому
натуральному числу
![]() ставится
в соответствие по некоторому закону
функция
ставится
в соответствие по некоторому закону
функция
![]() ,
определенная на множестве
,
определенная на множестве
![]() ,
то говорят, что на множестве
,
то говорят, что на множестве
![]() задана
функциональная последовательность
задана
функциональная последовательность
![]() .
Множество
называется
областью определения последовательности
.
.
Множество
называется
областью определения последовательности
.
Определение.
сходится
в точке
![]() ,
если числовая последовательность
,
если числовая последовательность
![]() сходится.
Множество всех точек
в
которых
сходится,
называется областью сходимости
функциональной последовательности
.
сходится.
Множество всех точек
в
которых
сходится,
называется областью сходимости
функциональной последовательности
.
![]() -
область сходимости
.
Пусть
-
область сходимости
.
Пусть
![]() -
обозначение предельного значения.
Совокупность всех предельных значений
есть функция, определенная на множестве
.
Эта функция
-
обозначение предельного значения.
Совокупность всех предельных значений
есть функция, определенная на множестве
.
Эта функция
![]() называется
предельной функцией последовательности
.
называется
предельной функцией последовательности
.
Замечание. Точечная сходимость на некотором множестве не гарантирует сохранения свойств членов последовательности (например, свойства непрерывности, интегрируемости и т.д.)
Функциональные ряды
Пусть
дана функциональная последовательность
![]() определенная
на множестве
.
определенная
на множестве
.
Формальное
выражение вида
![]() называется
функциональным рядом.
называется
функциональным рядом.
Множество
-
область определения ряда. Сумма
первых
членов ряда
![]() называется
-ой
частичной суммой функционального ряда.
Заметим, что
называется
-ой
частичной суммой функционального ряда.
Заметим, что
![]() является
функциональной последовательностью,
определенной на
.
является
функциональной последовательностью,
определенной на
.
Пусть
точка
![]()
Определение.
Функциональный
ряд
![]() сходится
в точке
,
если числовой ряд
сходится
в точке
,
если числовой ряд
![]() сходится.
Множество
точек
,
где
сходится,
называется областью сходимости ряда.
сходится.
Множество
точек
,
где
сходится,
называется областью сходимости ряда.
Определение.
Функциональный
ряд
сходится
на множестве
,
если последовательность
![]() его
частичных сумм сходится на
.
его
частичных сумм сходится на
.
Если
функциональный ряд сходится на множестве
,
то его сумма есть функция
![]() ,
определенная на
.
Очевидно,
есть
предел функциональной последовательности
.
,
определенная на
.
Очевидно,
есть
предел функциональной последовательности
.
Замечание. Поточечная сходимость ряда на множестве не гарантирует сохранения свойств членов ряда для сумм ряда.
Равномерная сходимость
Определение.
Последовательность
сходится
равномерно к функции
на
множестве
![]() ,
если
,
если
![]() .
(
.
(![]() не может быть одной точкой).
не может быть одной точкой).
Замечание. Из равномерной сходимости на множестве следует обычная (точечная) сходимость этой же последовательности на . Обратное неверно.
Определение.
Последоваельность
сходится
равномерно на
,
если существует
,
такая что
сходится
равномерно к
на
.
Обозначается
![]() на
.
на
.
Степенным
рядом
называется функциональный ряд вида
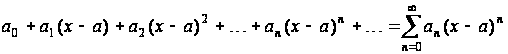 .(1.1)
.(1.1)
Здесь
![]() –
постоянные вещественные числа,
называемыекоэффициентамистепенного
ряда; а – некоторое постоянное число,
х –переменная,принимающая значения из
множества действительных чисел.
–
постоянные вещественные числа,
называемыекоэффициентамистепенного
ряда; а – некоторое постоянное число,
х –переменная,принимающая значения из
множества действительных чисел.
При
![]() степенной
ряд(1.1) принимает вид
степенной
ряд(1.1) принимает вид
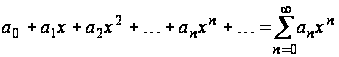 .
(1.2)
.
(1.2)
Степенной
ряд(1.1) называют рядом по степеням
разности
![]() ,ряд
(1.2) – рядом по степеням х.
,ряд
(1.2) – рядом по степеням х.
(Теорема Абеля):
если
степенной ряд (1.2) сходится при
![]() ,то
он абсолютно сходится при всех значениях
х, удовлетворяющих неравенству
,то
он абсолютно сходится при всех значениях
х, удовлетворяющих неравенству![]() ;если
же ряд(1.2) расходится при
,то
он расходится при всех значениях х,
удовлетворяющих неравенству
;если
же ряд(1.2) расходится при
,то
он расходится при всех значениях х,
удовлетворяющих неравенству![]() .
.
Теорема Абеля дает ясное представление о структуре области сходимости степенного ряда.
