13.6 Кинематика буровых насосов.
Основная задача кинематики буровых насосов — определение перемещения, скорости и ускорения поршня. Кинематическому анализу предшествует выбор геометрических параметров криво- шипношатунного механизма согласно заданным техническим показателям и характеристике проектируемого насоса. Радиус кривошипа принимается равным половине длины хода поршня. Длина шатуна выбирается с учетом возможности проворачивания кривошипа, габаритов насоса и угла передачи. Образуемого шатуном и перпендикуляром к направляющей ползуна. От угла передачи μ, зависит усилие в шатуне R, возникающее в результате разложения действующих на ползун сил сопротивлений (рис.13.20)
Угол передачи μ зависит от соотношения длин кривошипа и шатуна. Укорочение шатуна позволяет сократить длину бурового насоса, но приводит к уменьшению угла передачи. В связи с этим возрастает усилие в шатуне, что обусловливает необходимость увеличения площадей сечения и масс звеньев кривошипно-шатунного механизма. Это неблагоприятно влияет на динамику бурового насоса.
Вследствие жесткой кинематической связи, осуществляемой посредством штока, движения ползуна и поршня совпадают. Поэтому движение поршня описывается формулами, известными из кинематики кривошипно-шатунного механизма. При равномерном вращении угол поворота кривошипа за промежуток времени t составит
φ=ωt,
где φ—угол поворота, рад; ω—угловая скорость кривошипа, рад/с; t—время, с.
Ползун и поршень при повороте кривошипа на угол φ перемещаются из крайнего левого положения на расстояние
x=(r+ ℓ)-ВО,
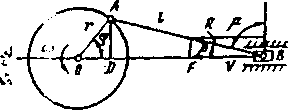
Где r- радиус кривошипа; ℓ - длина шатуна; ВО=ВD+DO= ℓ cosβ+rcosφ; β— угол наклона шатуна.
Рис. 13.20. Схема действия сил в кривошипно- шатунном механизме.
После обстановки значения BO получим
x = r + ℓ -( ℓ cosβ+r cosφ)= r (1-cosφ)+ℓ (1-cosβ). (13.20)
В практических расчетах пользуются приближенной формулой перемещения поршня. Из рассмотрения треугольников BAД и АОД имеем
r sinφ = ℓ sinβ,
откуда
sinβ
=
sinφ
тогда
cosβ=
=
Полученный радикал разлагается в ряд
Cosβ=
=1-
В
буровых
насосах отношение длин кривошипа и
шатуна изменяется в пределах:
При
:
,
второй член полученного ряда достигает
наибольшего значения при sinφ=l
и равен 0,02, а третий — 0,0002. Пренебрегая
этими членами ряда из-за
их малой величины, получаем более простую
формулу для определения
перемещения поршня:
x = r (l - cosφ). (13.21)
Из формулы (13.21) скорость движения поршня
, (13.22)
так как
.
Ускорение движения поршня
. (13.23)
По аналогии из формулы (13.23) можно получить более точные выражения для скорости и ускорения поршня, учитывающие длину шатуна:
;
.
Эксцентриковый вал образуется путем увеличения размеров цапфы, находящейся в точке А, за пределы оси вращения О (рис.13.20): R> r, где R— радиус эксцентрика; r—радиус кривошипа.
Радиус кривошипа в механизме эксцентрика называется эксцентриситетом. Кинематика эксцентрикового механизма от диаметра самого эксцентрика (диска) не зависит и описывается формулами, полученными для кривошипного вала.
В идеально работающем насосе жидкость безотрывно следует за поршнем и при бесконечно малом его перемещении dx подача насоса.
, (13.24)
где
-
площадь поршня.
Так как
то согласно формуле (13.22)
.
Подставляя, полученное значение dx в выражение (13.24), получаем
. (13.25)
Из уравнения (13.25) следует, что при равномерном вращении кривошипа подача жидкости, как и скорость поршня, изменяется то синусоиде. Объемная подача однопоршневого насоса одностороннего действия за ход нагнетания
где S=2 r- ход поршня.
Мгновенные значения подачи определяются текущей скоростью поршня
где
—
текущая скорость поршня;
—
текущий угол поворота кривошипа.
Наибольшего
значения мгновенная подача достигает
при повороте кривошипа на угол
/2:
где Т=60/n период одного оборота кривошипа.
При значениях угла поворота 0 и подача равна нулю:
Среднее значение подачи за один оборот кривошипа
=
2Fr/T.
Отношения предельных значений мгновенной подачи к средней мгновенной подаче равны:
Отношение разности предельных значений мгновенной подачи к средней ее величине характеризует неравномерность подачи и называется коэффициентом неравномерности подачи, который для однопоршневого насоса одностороннего действия, согласно полученным данным, составляет
(13.26)
В двухпоршневых насосах двустороннего действия коэффициент неравномерности подачи определяется по формуле
(13.27)
где d— диаметр штока; D — диаметр поршня.
Значения коэффициента неравномерности подачи двухпоршневого насоса двустороннего действия, полученные по формуле(13.27), приведены ниже.
d/D - 0,2 0,3 0,4 0,5 0,6
0,35 0,41 0,48 0,58 0,65
Как видно, с увеличением отношения d/D коэффициент неравномерности подачи возрастает. Из этого следует, что в двухпоршневых буровых насосах двустороннего действия неравномерность подачи увеличивается с уменьшением диаметра сменных втулок, так как диаметр штока при этом не изменяется.