2.1.2. Активные фильтры
Активным называется фильтр, содержащий один или несколько активных четырехполюсников (ЧП) с обратной связью, за счет которой формируется амплитудно-частотная характеристика (АЧХ) фильтра. Если в схеме фильтра не содержится индуктивностей, то его называют активным RC-фильтром, или ARC-фильтром. Широкое применение ARC-фильтров обусловлено рядом их преимуществ перед пассивными фильтрами: возможностью микроминиатю-ризации, невысокой стоимостью и простотой изменения параметров передачи. Наличие операционного усилителя в схеме ARC-фильтра позволяет получать сигнал на выходе фильтра с некоторым усилением.
Технические требования к активным фильтрам основываются на задании амплитудно-частотной характеристики или частотной характеристики ослаб-ления. Переход от рабочей постоянной передачи к рабочей передаточной функции выполняется по формуле:
.
(2.4)
Если
,
то рабочую передаточную функцию называют
системной:
.
(2.5)
Модуль выражения (2.5) представляет собой амплитудно-частотную характеристику (АЧХ) фильтра.
В
зависимости от количества реактивных
элементов в схеме пассивного фильтра
в выражении (2.4) можно получить различные
степени оператора р.
Простейшие фильтры нижних и верхних
частот, состоящие из одного реактивного
элемента и резистора, являются фильтрами
первого порядка; полузвенья ФНЧ и ФВЧ
типа k
– второго порядка, а полузвенья типа
m
–третьего порядка. Схемы и расчетные
формулы для определения
фильтров типа k
приведены в табл. 2.2, типа m
– в табл. 2.3. Такие же формулы для
системной функции можно получить и с
помощью (А)-пара-метров соответствующих
схем.
Следует
отметить, что при
и
исследуемого четырехполюсника его
собственное ослабление, Нп, рассчитывается
по формуле:
.
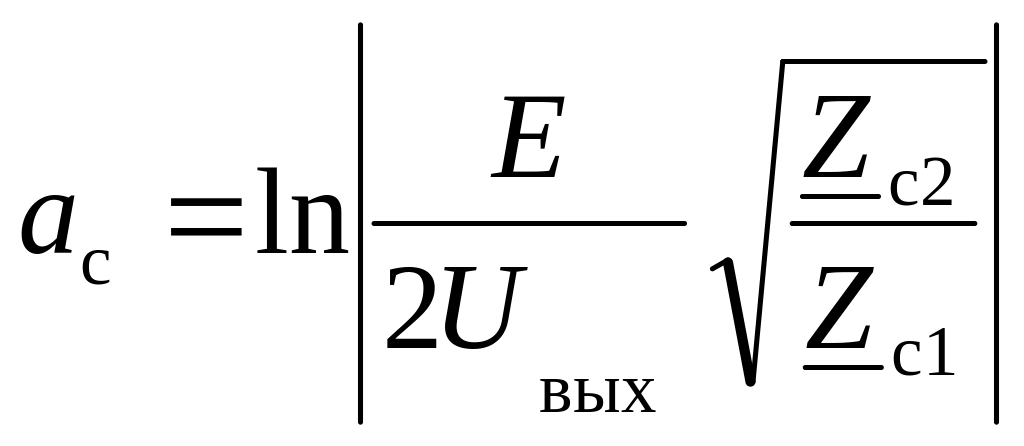(2.6)
При
синтезе схем ARC-фильтра
передаточную функцию (
или
)
раскладывают на несколько сомножителей
и реализуют цепочечно соединяемыми
каскадами. С этой целью вычисляют корни
полиномов числителя и знаменателя и
для каждой пары комплексно сопряженных
корней определяют трехчлен вида
.
В
случае нечетной степени полинома
числителя (знаменателя) в выражении
(2.6) появляется двучлен
,
в котором может отсутст- вовать
частота
.
Для реализации передаточных функций второго порядка необходимо применять схемы с операционным усилителем, функцию первого порядка можно реализовать с помощью RC-цепи.
Наиболее распространенные схемы ФНЧ и ФВЧ и расчетные формулы см. в табл. 2.2 и 2.3. Для реализации полузвеньев фильтров типа k используются одно- и двухпетлевые цепи обратной связи (см. табл. 2.2), а при реализации фильтра типа m каскадно соединяют фильтр первого порядка с заградительным фильтром второго порядка (см. табл. 2.3).
Пример расчета элементов фильтра типа m приведен в приложении.
