3. Анализ схем четырехполюсников

3.1. Определение основной матрицы исследуемого четырехполюсника

В курсовой работе рассматривается ЧП, собранный из оптимально выбранных ДП в соответствии со схемой замещения, указанной в задании на курсовую работу. Схема замещения бывает Г-, Т-, П-образной, а также мостовой симметричной.

Теория ЧП позволяет, применяя некоторые обобщенные параметры, связать между собой напряжения и токи на входе и выходе, не производя расчетов этих величин в схеме самого ЧП. К таким обобщенным параметрам, в частности, относятся собственные параметры ЧП, которые определяются без учета влияния внешних подключений (генератора и нагрузки):

1) коэффициенты A, B, Z, Y, H, G;

2) характеристические параметры Z_с1, Z_с2, g_с;

3) повторные параметры Z_п1, Z_п2, g_п.

Имеются различные формулы связи собственных параметров между собой. Наиболее часто на практике используются параметры А и характе-ристические.

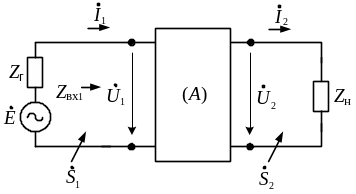
Четырехполюсную цепь (рис. 3.1), имеющую вход и выход, следует характеризовать связями между двумя напряжениями ( и ) и двумя токами ( и ). Эти связи представляют различным образом в зависимости от того, какие две из четырех величин заданы и какие две подлежат определению. При этом образуется система уравнений с двумя неизвестными. Такую систему уравнений для любых заданных условий включения ЧП можно дополнить еще двумя: уравнением генератора – и приемника – .

Если за функции принять напряжение и ток , а за аргументы – и , то получим основную систему уравнений ЧП, А-параметры которой чаще всего используются в теоретических расчетах:

(3.1)

В матричной форме система (3.1) имеет вид:

.

(3.2)

а	б

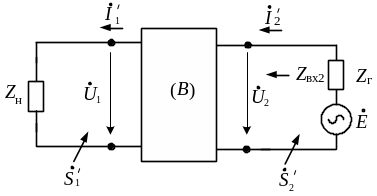
Рис. 3.1. Схема четырехполюсника:

а – прямое направление передачи; б – обратное

Физический смысл и один из способов определения А-параметров следуют из опытов холостого хода (х. х.) и короткого замыкания (к. з.) ЧП.

При = 0 (х. х.)

; (3.3) . (3.4)

При = 0 (к. з.)

; (3.5) . (3.6)

Для пассивных ЧП определитель, составленный из А-параметров, равен единице:

.

(3.7)

Только три параметра ЧП могут быть заданы независимо друг от друга, а четвертый определяется из уравнения связи (3.7). Если ЧП симметричный, то А₁₁ = А₂₂, т. е. число независимых коэффициентов остается равным двум.

При обратном направлении передачи энергии (см. рис. 3.1, б) используются параметры В.

В курсовой работе после выбора оптимальных схем ДП необходимо в соответствии с заданием составить одну из канонических схем ЧП, записать аналитические выражения для А-параметров и рассчитать их при одном значении частоты, проверив выполнения равенства (3.7).

3.2. Определение коэффициентов одной формы уравнений через коэффициенты другой формы

Если заданными величинами являются токи и ЧП (см. рис. 3.1), а неизвестными – напряжения и , то получим систему Z-параметров:

.

(3.8)

При этом = – .

Аналогично можно получить и другие системы параметров ЧП:

; (3.9) ; (3.10)

; (3.11) . (3.12)

Существуют топологические методы расчета электрических схем, которые основаны на аналитическом или графическом способе описания свойств графа, изображающего электрическую цепь.

В курсовой работе с помощью теории направленных графов необходимо получить соотношения между параметрами-коэффициентами ЧП. При этом следует руководствоваться правилами преобразования графа:

1) параллельно соединенные ветви, направленные в одну сторону, заме-няются одной ветвью, коэффициент передачи которой равен сумме коэффициентов передачи параллельно соединенных ветвей;

2) последовательные ветви, направленные в одну сторону, заменяются одной с коэффициентом передачи, равным произведению коэффициентов передач заменяемых ветвей;

3) графы можно инвертировать, т. е. изменять направление передачи.

Порядок инверсии:

а) изменяется направление ветви на противоположное, а коэффициент передачи заменяется обратным;

б) все ветви, входящие в тот же узел, что и инвертируемая ветвь, переносятся в узел, в который она входит, с сохранением коэффициента передачи от узла к узлу, но с изменением знака коэффициента передачи;

в) устраняются промежуточные узлы и параллельные передачи от истока к стоку.

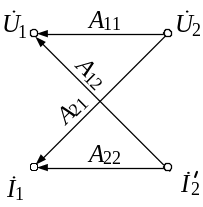
В качестве примера преобразуем граф Z-матрицы, чтобы получить граф А-матрицы, т. е. выразим А-параметры через Z-параметры (рис. 3.2).

а	б
в	г
д	е

Рис. 3.2. Преобразование параметров четырехполюсника методом графа:

а – е – этапы преобразования графа

Дано:

Требуется получить зависимости:

Инвертируем ветвь Z₂₁ в исходном графе (рис. 3.2, а), в итоге получаем граф, представленный на рис. 3.2, б. Устраняем промежуточный узел. Соединенные последовательно ветви от узлов и к узлу через узел заменяем прямыми ветвями. При этом коэффициенты передачи соответствующих ветвей перемножаются (рис. 3.2, г), а ветвь с коэффициентом передачи Z₁₁ устраняется. Затем заменяем две параллельные ветви от узла к узлу одной. При этом коэффициенты передачи ветвей складываются (рис. 3.2, д). Наконец, меняем знаки передач ветвей, примыкающих к узлу , так как = – (рис. 3.2, е). Сравнивая графы, представленные на рис. 3.2, б и е, получаем следующее соотношение между А- и Z-параметрами ЧП:

.

(3.13)

Таким образом, если заданы Z-параметры, то из соотношения (3.13) можно получить А-параметры. Аналогично можно получить и остальные соотношения между параметрами ЧП.
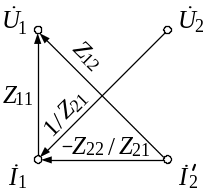
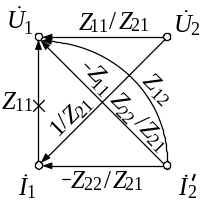
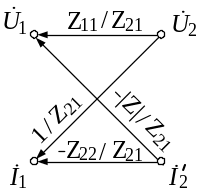
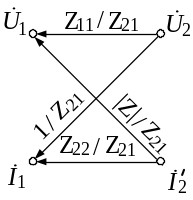
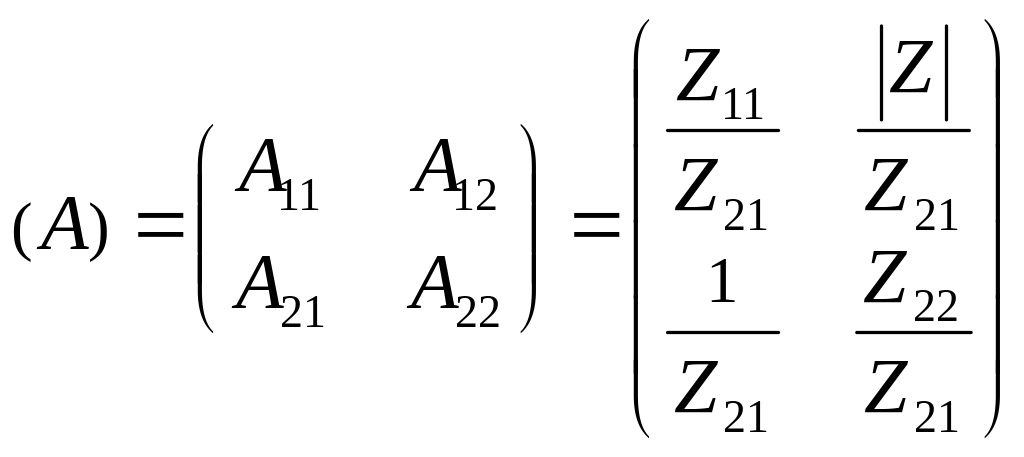