14.6.3. Поверхностные интегралы второго рода (пи-2)
Пусть: 1) в точках
двусторонней гладкой (или кусочно-глад-кой)
поверхности задана
ограниченная функция
;
2) выбрана положительная сторона
поверхности; 3)
– разбиение на n
частей
с площадями
и диаметрами
;
4)
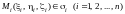– произвольный набор точек;
5)
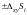– проекция элемента
на плоскость
(проекция определенной
стороны поверхности связана со знаком
« + » или « – »); 6)
–
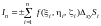интегральная сумма, соответствующая
данному разбиению и выбору точек.
Определение.
Конечный предел
при
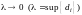называется поверхностным интегралом
второго рода от
по определенной стороне поверхности
:
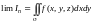
(здесь
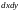напоминает о проекции
на
и содержит знак).
При
проектировании ориентированной
поверхности на
плоскост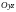и
и
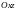получаем ПИ-2:
.
Вычисление пи-2
Теорема
14.11. Пусть ориентированная гладкая
поверхность
задана явно. Тогда
а)
если
,
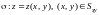то
;
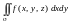
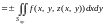(14.35а)
б)
если
,
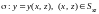то
;
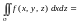
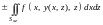(14.35б)
в)
если
,
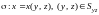то
.
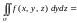
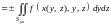(14.35в)
Связь между пи-1 и пи-2
Теорема
14.12. Если – гладкая
двусторонняя поверхность, ориентация
характеризуется
нормалью
=
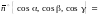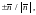
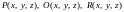– функции, определенные и непрерывные
на , то
.
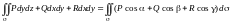(14.36)
Связь между ПИ-2 и тройным интегралом
(формула Гаусса – Остроградского)
Теорема
14.13. Пусть функции
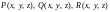– непрерывные вместе со своими частными
производными (первого порядка) в некоторой
пространственной области V,
ограниченной гладкой замкнутой
поверхностью с
положительной внешней стороной.
Справедлива формула
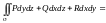
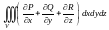
З а м е ч а н и е. О приложениях ПИ-2 смотри в разделе «Элементы теории поля».
Пример
25. Вычислить
ПИ-2:
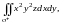где
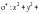
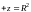– положительная (внешняя) сторона сферы.
Для вычисления
ПИ-2 замкнутую поверхность
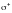необходимо
разбить на
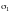с
уравнением
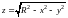и
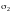с уравнением
(рис. 14.28). Тогда на основании (14.32)
положительная сторона поверхности
характеризуется
нормальным вектором
,
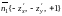ибо угол между
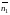и положительным на-
п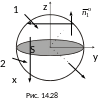
равлением
Oz, т.е. (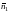
,Oz),
– острый, а положительная сторона
поверхност-
ности
– вектором
,
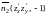ибо угол (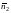
,Oz)
– тупой. Проекция каждой из поверхностей
и
есть область
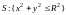– круг радиуса R с
центром в начале координат. Поэтому по
формуле (14.35а)
+
+
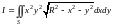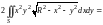перехо-
дим к полярным координатам:
,
=
=
=
=
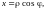
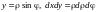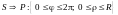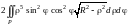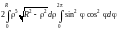=двойной
интеграл «расщепился» в произведение
определенных интегралов=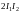
;
=
=
;
.
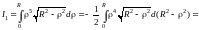
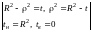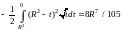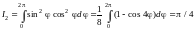Итак,
.
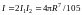Пример
26. Вычислить ПИ-2 общего вида:
,
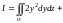
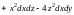где
– внешняя сторона конической поверхности
,
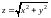ограниченной плоскостью z
= 2.
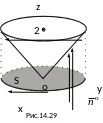Внешняя сторона
поверхности
характеризуется
нормальным вектором, который составляет
тупой угол с положительным направлением
оси Oz (рис. 14.29), а потому
=
,
=
=
.
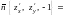
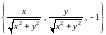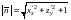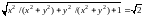Тогда
,
.
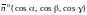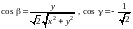Данный ПИ-2 можно вычислять по-разному. Первый способ – вычислять три ПИ-2, составляющих данный поверхностный интеграл. Второй способ – использовать связь ПИ-2 с ПИ-1, что и сделаем. По формуле (14.36)
=
=
=
.
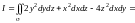
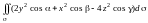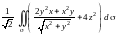Последний поверхностный интеграл есть
ПИ-1. Проекция
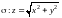на плоскость Oxy есть
область
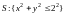– круг радиуса 2 с центром в начале
координат. Так как
,
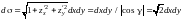то по формуле (14.33) (или (14.34))
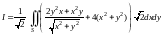=переходим
к полярным координатам:
=
=
=
=
=
=
.
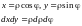
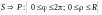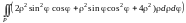
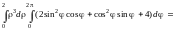
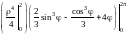
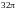