
- •14.1. Определение кратного интеграла.
- •14.2. Двойные интегралы
- •14.2.1. Области на плоскости
- •14.2.2. Повторный интеграл
- •14.2.4. Замена переменных в двойном интеграле
- •14.3. Тройные интегралы
- •14.3.1. Области в пространстве
- •3.2. Вычисление тройного интеграла
- •14.3.3. Замена переменных в тройном интеграле
- •Переход в тройном интеграле к цилиндрическим координатам
- •14.5. Криволинейные интегралы
- •14.5.1. Криволинейные интегралы первого рода (ки-1)
- •Вычисление ки-1
- •Некоторые приложения ки-1
- •14.5.2. Криволинейные интегралы второго рода (ки-2)
- •Вычисление ки-2
- •Следствия. А) Для плоской линии ab: и функций , :
- •Независимость ки-2 от пути интегрирования
- •Связь между ки-1 и ки-2
- •Связь ки-2 с двойным интегралом (формула Грина)
- •14.6. Поверхностные интегралы
- •14.6.1. Двусторонние поверхности и их ориентация
- •14.6.2. Поверхностный интеграл первого рода (пи-1)
- •Вычисление пи-1
- •Некоторые приложения пи-1
- •Задания. 1. Записать линейные свойства пи-1.
- •14.6.3. Поверхностные интегралы второго рода (пи-2)
- •Вычисление пи-2
- •Связь между пи-1 и пи-2
14.5.2. Криволинейные интегралы второго рода (ки-2)
Пусть:
1) в точках непрерывной кривой AB
из пространства
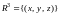 определены ограниченные скалярные
функции
определены ограниченные скалярные
функции
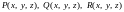 ;
2)
;
2)
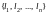 – произвольное разбиение кривой AB
на элементарные дуги
с
длинами
и проекциями
– произвольное разбиение кривой AB
на элементарные дуги
с
длинами
и проекциями
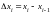 ,
,
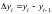 ,
,
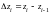 на соответствующие оси координат; 3)
на соответствующие оси координат; 3)
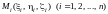 – произвольный набор точек; 4)
– произвольный набор точек; 4)
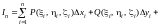
 –
интегральная
сумма, соответствующая данному разбиению
и данному выбору точек.
–
интегральная
сумма, соответствующая данному разбиению
и данному выбору точек.
Определение.
Конечный предел
интегральной суммы
при
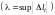 ,
не зависящий ни от способа разбиения
AB,
ни от выбора точек
,
называется криволинейным
интегралом вто-
,
не зависящий ни от способа разбиения
AB,
ни от выбора точек
,
называется криволинейным
интегралом вто-
рого
рода от функций
 по
пути AB:
по
пути AB:
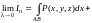
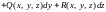 .
.
Механически
КИ-2 представляет собой работу
переменной силы
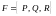 ,
точка приложения которой описывает
кривую AB.
,
точка приложения которой описывает
кривую AB.
Вычисление ки-2
Теорема
14.7. Если линия AB
задана в параметрической форме:
,
где
 –
непрерывно дифференцируемые функции,
и при изменении параметра t
от
–
непрерывно дифференцируемые функции,
и при изменении параметра t
от
 к
к
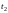 кривая описывается именно от точки A
к точке B, то
кривая описывается именно от точки A
к точке B, то
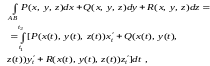
(14.28)
причем КИ-2 существует, если существует определенный интеграл.
Следствия. А) Для плоской линии ab: и функций , :
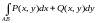
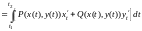 .
.
б)
Для заданной явно плоской линии

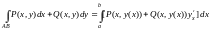 .
(14.29)
.
(14.29)
Независимость ки-2 от пути интегрирования
Теорема 14.8. Если функции непрерывны вместе со своими частными производными первого порядка в некоторой замкнутой ограниченной поверхностно односвязной области V, то равносильны следующие четыре утверждения:
1 )
)
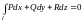 ,
где l – замкнутый
контур, лежащий внутри V;
,
где l – замкнутый
контур, лежащий внутри V;
2)
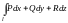 не зависит от выбора
пути интегрирования;
не зависит от выбора
пути интегрирования;
3)
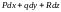 есть полный дифференциал некоторой
однозначной функции
есть полный дифференциал некоторой
однозначной функции
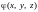 ,
заданной в точках V;
,
заданной в точках V;
4)
выполняются равенства:
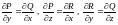 .
.
Функция может быть найдена, например, по формуле
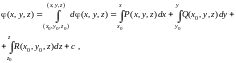 (14.30)
(14.30)
где
 –
некоторая фиксированная точка области
V, c
– произвольная постоянная.
–
некоторая фиксированная точка области
V, c
– произвольная постоянная.
Связь между ки-1 и ки-2
Пусть
спрямляемая (не имеющая особых точек)
линия AB имеет в каждой
точке касательную, положительное
направление которой составляет с осями
координат углы
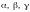 .
Тогда
.
Тогда
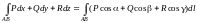 .
.
Связь ки-2 с двойным интегралом (формула Грина)
Теорема
14.9. Пусть: 1) функции
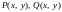 непрерывны и имеют непрерывные частные
производные в открытой односвязной
области
непрерывны и имеют непрерывные частные
производные в открытой односвязной
области
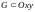 ;
2) l – кусочно-гладкий
контур, ограничивающий область
;
2) l – кусочно-гладкий
контур, ограничивающий область
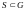 ,
и при положительном обходе l
ближайшая часть области S
находится слева от наблюдателя. Тогда
справедлива формула:
,
и при положительном обходе l
ближайшая часть области S
находится слева от наблюдателя. Тогда
справедлива формула:
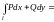
 .
.
Площадь плоской области. Площадь s фигуры S, ограниченной простым кусочно-гладким контуром l, равна
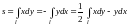 .
.
Пример
20. Вычислить КИ-2
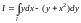 ,
где L – дуга параболы
,
где L – дуга параболы
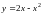 ,
проходимая от точки
,
проходимая от точки
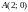 до точки
.
до точки
.
Кривая
l
представлена на рис. 14.24. По формуле
(14.29) имеем
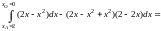
= .
.
Пример
21. Вычислить КИ-2
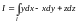 ,
где l – замкнутый
контур, полученный пересечением сферы
,
где l – замкнутый
контур, полученный пересечением сферы
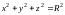 и цилиндра
и цилиндра
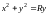
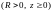 ,
обходимый против часовой стрелки, если
смотреть из начала координат (рис.
14.25).
,
обходимый против часовой стрелки, если
смотреть из начала координат (рис.
14.25).

Для вычисления
КИ-2 представим l в
параметрической форме. Поверхность
запишем
в виде
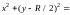
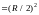 .
Последнее равенство
выполнится тождественно,
если
положить, например,
.
Последнее равенство
выполнится тождественно,
если
положить, например,
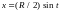 ,
,
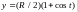 ,
.
Тогда из уравнения сферы имеем
,
.
Тогда из уравнения сферы имеем
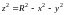 =
=
=
=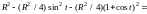
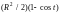 =
= .
Отсюда, помня, что
.
Отсюда, помня, что
 ,
имеем
,
имеем
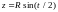 .
Итак,
.
Итак,
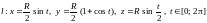 ;
;
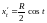 ,
,
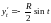 ,
,
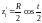 .
По формуле (14.28)
.
По формуле (14.28)
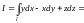 =
=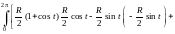
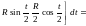
=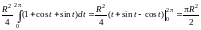 .
.
Пример
22. Найти первообразную функции
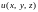 ,
если
,
если
 .
.
По формуле (14.30)
при
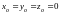 получим
получим
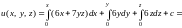
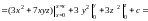
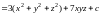 .
.
