14.5. Криволинейные интегралы

14.5.1. Криволинейные интегралы первого рода (ки-1)

Пусть: 1) в точках простой (без точек самопересечения), спрямляемой (т.е. имеющей длину) кривой l из пространства

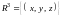определена ограниченная скалярная функция 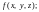2) 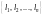– произвольное разбиение кривой l на элементарные дуги 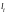с длинами 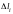; 3) 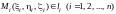– произвольный набор точек; 4)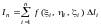 – интегральная сумма, соответствующая данному разбиению кривой l и выбору точек .

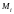Определение. Конечный предел интегральной суммы при 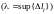, не зависящий ни от способа разбиения кривой l, ни от выбора точек , называется криволинейным интегралом первого рода от функции 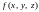по кривой l:

.

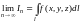Вычисление ки-1

Теорема 14.6. Если кривая l задана параметрическими уравнениями: 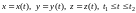, где 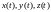– непрерывно дифференцируемые по t функции и возрастание длины L дуги кривой соответствует возрастанию t, то в предположении существования определенного интеграла имеет место равенство

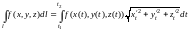
(14.24)

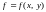Следствия. а) Если плоская кривая l задана явно: , и , то

;

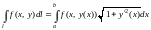(14.25)

б) Если плоская кривая l задана в полярных координатах: 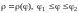, то

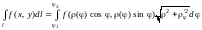
(14.26)

Некоторые приложения ки-1

1. Масса материальной линии. Пусть 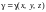, 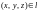– линейная плотность массы материальной линии l. Тогда масса этой линии есть:

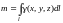. (14.27)

2. Длина пространственной (или плоской) кривой l есть L:

.

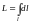3. Статические моменты и координаты центра тяжести.

а) Для плоской линии 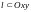c плотностью и массой m статические моменты относительно координатных осей Oy и Ox:

, ;

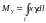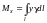координаты центра тяжести:

, .

б) Для пространственной линии l c плотностью и массой m статические моменты относительно плоскостей и Oxy:

, , ;

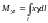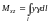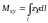координаты центра тяжести:

, , .

Пример 17. Вычислить КИ-1 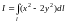, где l – прямолинейный отрезок, соединяющий точки 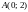и .

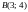 Уравнения отрезка прямой AB в параметрической форме: 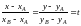, 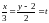или 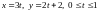. Тогда 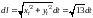и из (14.24) имеем =

= .

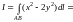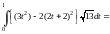
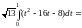
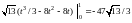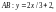
З а м е ч а н и е. В случае явного задания отрезка прямой 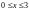следует воспользоваться формулой (14.25). 

П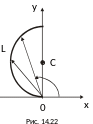 ример 18. Вычислить КИ-1 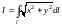, где l – кривая, заданная уравнением 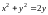при условии .

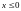 Для построения кривой l преобразуем уравнение ее к виду 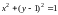; таким образом, l есть полуокружность с центром в точке 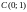радиуса 1, расположенная слева от оси Oy (рис. 14.22).

Наличие комбинации в подынтегральной функции и в уравнении l наводит на мысль провести вычисления в полярных координатах, которые связаны с декартовыми координатами формулами

.

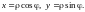Т огда из получаем 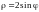– уравнение l в поляр-ных координатах; из рис. 14.22 (или условий , 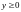, 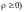следует ;

;

= =

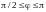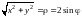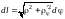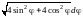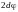= , и из (14.26)

= . 

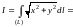
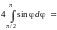
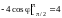Пример 19. Найти массу одного витка материальной винтовой линии 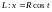, , 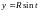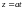(рис. 14.23), если линейная плотность в точке обратно пропорциональна квадрату расстояния этой точки от начала координат.

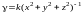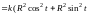
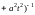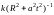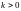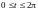 По условию задачи плотность = = , где k – коэффициент проп орциональности, . Для одного витка . Из формул (14.27) и (14.24) имеем:

=

= =

. 
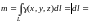
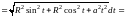
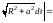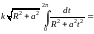
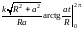
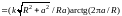